 Géométrie repérée
Géométrie repérée
Quelques rappels de seconde pour commencer
Définition
Deux vecteurs sont colinéaires si et seulement si
- soit l'un des deux vecteurs est nul
- soit les deux vecteurs ont la même direction.
Propriété
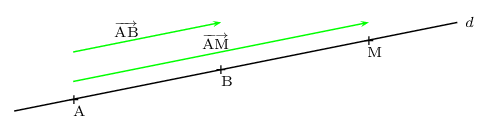
Soient A et B deux points distincts d'une droite $d$.
M appartient à la droite $d$ si et seulement si il existe un nombre réel $k$ tel que ${AM}↖{→}=k{AB}↖{→}$.
${AB}↖{→}$ est un vecteur directeur de la droite $d$.
Remarque:
Une droite peut être définie par 2 points distincts.
Une droite peut être définie par un point et un vecteur directeur (nécessairement non nul).
Propriété
Deux droites sont parallèles
si et seulement si elles ont des vecteurs directeurs colinéaires.
Propriété
Le plan est muni d'un repère $(O,{i}↖{→},{j}↖{→})$.
Soit ${u}↖{→}(x\,;\,y)$ et ${v}↖{→}(x'\,;\,y')$ deux vecteurs et $λ$ un réel.
alors: ${u}↖{→}+{v}↖{→}\,(x+x'\,;\,y+y')$ et
$λ{u}↖{→}\,(λx\,;\,λy)$.
Soit $A(x_A\,;\,y_A)$ et $B(x_B\,;\,y_B)$ deux points du plan.
alors: $${AB}↖{→}\,(x_B-x_A\,;\,y_B-y_A)$$;
si $I(x_I;y_I)$ est le milieu de [AB],
alors: $x_I={x_A+x_B}/{2}$ et $y_I={y_A+y_B}/{2}$ .
Définition
Le plan est muni d'un repère $(O,{i}↖{→},{j}↖{→})$.
Soit ${u}↖{→}(x\,;\,y)$ et ${v}↖{→}(x'\,;\,y')$ deux vecteurs.
Le déterminant du couple $({u}↖{→};{v}↖{→})$ est le réel $xy'-x'y$
Propriété
Le plan est muni d'un repère $(O,{i}↖{→},{j}↖{→})$.
Soit ${u}↖{→}(x\,;\,y)$ et ${v}↖{→}(x'\,;\,y')$ deux vecteurs
Les vecteurs ${u}↖{→}$ et ${v}↖{→}$ sont colinéaires si et seulement si le déterminant du couple $({u}↖{→};{v}↖{→})$ est nul.
Propriété
Le plan est muni d'un repère orthonormé $(O,{i}↖{→},{j}↖{→})$.
Si ${u}↖{→}(-b\,;\,a)$ est un vecteur directeur de la droite $d$,
alors $d$ admet une équation cartésienne du type $ax+by+c=0$.
Réciproquement, l'ensemble des points dont les coordonnées vérifient l'égalité $ax+by+c=0$ (avec $a$ et $b$ non nuls ensemble)
est une droite de vecteur directeur ${u}↖{→}(-b\,;\,a)$.
Voici ci-dessous le cours de première.
Définition
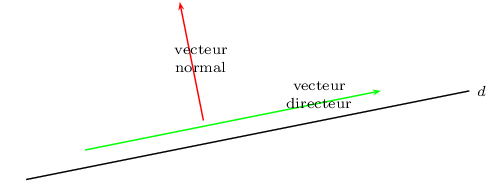
Un vecteur normal à une droite $d$ est un vecteur non nul orthogonal à un vecteur directeur de $d$.
Propriété
Un vecteur normal à une droite $d$ est orthogonal à tout vecteur directeur de $d$.
Si ${n}↖{→}$ est un vecteur normal à la droite $d$, alors tout vecteur non nul orthogonal à ${n}↖{→}$ est un vecteur directeur de $d$.
Propriété
Le plan est muni d'un repère orthonormé $(O,{i}↖{→},{j}↖{→})$.
Si ${n}↖{→}(a\,;\,b)$ est un vecteur normal à la droite $d$,
alors $d$ admet une équation cartésienne du type $ax+by+c=0$.
Réciproquement, l'ensemble des points dont les coordonnées vérifient l'égalité $ax+by+c=0$ (avec $a$ et $b$ non nuls ensemble) est une droite de vecteur normal
${n}↖{→}(a\,;\,b)$.
 Exemple
Exemple
Le plan est muni d'un repère orthonormé $(O,{i}↖{→},{j}↖{→})$.
Soit $A(2;3)$ un point et ${v}↖{→}(4;5)$ un vecteur.
Soit $d$ la droite passant par A et de vecteur normal ${v}↖{→}$.
Donner un vecteur directeur ${w}↖{→}$ de la droite $d$.
Pour chaque équation qui suit, déterminer s'il s'agit d'une équation de la droite $d$.
- $-5x+4y-2=0$
- $4x+5y-22=0$
- $-2x-2,5y+11,5=0$
- $y=-0,8x+4,6$
Corrigé
${v}↖{→}(4;5)$ est un vecteur normal à $d$.
On définit alors le vecteur ${w}↖{→}(-5;4)$ (les coordonnées sont inversées, et l'une d'elles change de signe)
Ce vecteur ${w}↖{→}$ est alors orthogonal au vecteur ${v}↖{→}$ (en effet: ${v}↖{→}.{w}↖{→}=xx'+yy'=-5×4+4×5=0$).
Et comme ${v}↖{→}$ est normal à $d$, le vecteur non nul ${w}↖{→}$ est un vecteur directeur de $d$.
Déterminons si les équations qui suivent concernent la droite $d$.
- $-5x+4y-2=0$ est l'équation d'une droite de vecteur normal ${w}↖{→}(-5;4)$.
Or ce vecteur est un vecteur directeur de $d$, et il n'est donc pas normal à $d$.
Donc cette équation ne concerne pas $d$.
En fait, c'est l'équation d'une droite perpendiculaire à $d$. - $4x+5y-22=0$ est l'équation d'une droite de vecteur normal ${v}↖{→}(4;5)$, qui est bien un vecteur normal à $d$.
Mais $4x_A+5y_A-22=4×2+5×3-22=1$
Le résultat n'est pas nul. Donc A n'appartient pas à cette droite.
Donc cette équation ne concerne pas $d$.
- $-2x-2,5y+11,5=0$ est l'équation d'une droite de vecteur normal ${n}↖{→}(-2;-2,5)$.
Or le vecteur non nul ${n}↖{→}$ est orthogonal à un vecteur directeur de $d$ (en effet: ${n}↖{→}.{w}↖{→}=-2×(-5)-2,5×4=0$).
Donc ${n}↖{→}$ est un vecteur normal à $d$.
De plus, $-2x_A-2,5y_A+11,5=-2×2-2,5×3+11,5=0$
Donc A appartient à cette droite.
Donc cette équation est une équation cartésienne de $d$. - La droite $d'$ d'équation réduite $y=-0,8x+4,6$ a pour vecteur directeur ${u}↖{→}(1;-0,8)$
Or, comme ${u}↖{→}.{v}↖{→}=xx'+yy'=1×4+(-0,8)×5=0$, le vecteur ${v}↖{→}(-5;4)$ est orthogonal à un vecteur directeur de $d'$.
Donc ${v}↖{→}$ est un vecteur normal à $d'$.
De plus, $-0,8x_A+4,6=-0,8×2+4,6=3=y_A$
Donc A appartient à cette droite $d'$.
Donc $d$ et $d'$ sont confondues.
Donc cette équation est l'équation réduite de $d$.
Propriété
Le plan est muni d'un repère orthonormé $(O,{i}↖{→},{j}↖{→})$.
Soit $A(x_A\,;\,y_A)$ un point et $r$ un réel positif.
Soit $\C$ le cercle de centre A et de rayon $r$.
Le point $M(x\,;\,y)$ appartient à $\C$ si et seulement si
${(x-x_A)}^2+{(y-y_A)}^2=r^2$
Ceci s'appelle une équation du cercle $\C$.
 Exemple
Exemple
Le plan est muni d'un repère orthonormé $(O,{i}↖{→},{j}↖{→})$.
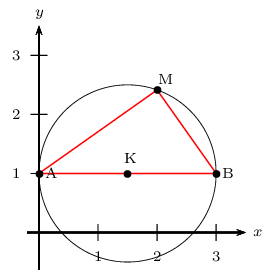
Soit $A(0;1)$, $B(3;1)$ et $M(2;1+√{2})$ trois points.
- Montrer que l'équation (E): $x^2-3x+y^2-2y+1=0$ est celle d'un cercle $\C$ dont on donnera le centre $K$ et le rayon $r$.
- Montrer que M est sur ce cercle $\C$.
- Déterminer une équation du cercle $\C'$ de diamètre [AB].
- Que dire du triangle ABM?
Corrigé
-
Nous allons écrire l'équation proposée sous la forme ${(x-x_K)}^2+{(y-y_K)}^2=r^2$ en appliquant la méthode de complétion du
carré.
(E) $ ⇔$ $x^2-3x+y^2-2y+1=0$ $ ⇔$ $x^2-2×x×1,5+1,5^2-1,5^2+y^2-2×y×1+1^2-1^2+1=0$
Soit: (E) $ ⇔$ $(x-1,5)^2-2,25+(y-1)^2-1+1=0$
Soit: (E) $ ⇔$ $(x-1,5)^2+(y-1)^2=2,25$
Donc (E) est l'équation du cercle $\C$ de centre $K(1,5;1)$ et de rayon $r=√{2,25}$. -
On a: $(x_M-1,5)^2+(y_M-1)^2=(2-1,5)^2+(1+√{2}-1)^2=0,25+2=2,25$
Donc M est sur le cercle $\C$. - Soit $N(x;y)$. On a alors: ${AN}↖{→}(x;y-1)$ et ${BN}↖{→}(x-3;y-1)$.
$N(x;y)$ est sur $\C'$ $ ⇔$ ${AN}↖{→}.{BN}↖{→}=0$.
$N(x;y)$ est sur $\C'$ $ ⇔$ $x(x-3)+(y-1)(y-1)=0$.
$N(x;y)$ est sur $\C'$ $ ⇔$ $x^2-3x+y^2-2y+1=0$.
Ceci est donc une équation de $\C'$.
On retrouve l'équation (E). Donc les cercles $\C$ et $\C'$ sont confondus. - Le point M est donc un point du cercle de diamètre [AB] (distinct de A et de B).
Donc le triangle ABM est rectangle en M.