 Dérivation
Dérivation
I. Nombre dérivé
Définition
La droite d'équation $y=ax+b$ admet pour coefficient directeur le nombre $a$.
Soit $x_A≠x_B$; la droite passant par les points A($x_A$;$y_A$) et B($x_B$;$y_B$) admet
pour coefficient directeur le nombre ${y_B-y_A}/{x_B-x_A}$.
Définition et propriété
Soit $f$ une fonction définie sur un intervalle I. Soit $x_0$ et $x_1$ deux réels distincts appartenant à I.
Le taux de variation (ou taux d'accroissement) de $f$ entre $x_0$ et $x_1$ est le nombre ${f(x_1)-f(x_0)}/{x_1-x_0}$.
Il est égal au coefficient directeur de la "corde" passant par $A(x_0; f(x_0))$ et $B(x_1; f(x_1))$.
 Exemple
Exemple
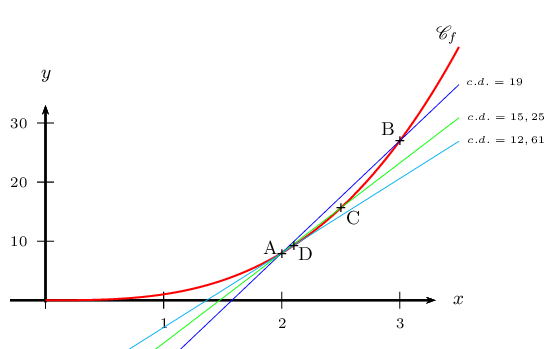
Soit $f$ la fonction définie par $f(x)=x^3$.
Calculer le taux d'accroissement de $f$ entre $2$ et $3$, puis entre $2$ et $2,5$ puis entre $2$ et $2,1$.
Interpréter graphiquement.
Corrigé
Le taux d'accroissement de $f$ entre $2$ et $3$ vaut ${f(3)-f(2)}/{3-2}={27-8}/{1}=19$
La corde passant par $A(2;8)$ et $B(3;27)$ a pour coefficient directeur $19$.
Le taux d'accroissement de $f$ entre $2$ et $2,5$ vaut ${f(2,5)-f(2)}/{2,5-2}={15,625-8}/{0,5}=15,25$
La corde passant par $A(2;8)$ et $C(2,5;15,625)$ a pour coefficient directeur $15,25$.
Le taux d'accroissement de $f$ entre $2$ et $2,1$ vaut ${f(2,1)-f(2)}/{2,1-2}={9,261-8}/{0,1}=12,61$
La corde passant par $A(2;8)$ et $D(2,1;9,261)$ a pour coefficient directeur $12,61$.
Définition
Soit $r(h)$ une fonction.
S'il existe un nombre réel $l$ tel que $r(h)$ devienne aussi proche de $l$ que l'on veut pourvu que $h$ soit suffisamment proche de $0$, alors on dit que:
la limite de $r(h)$ quand $h$ tend vers 0 vaut $l$.
On note: $ \lim↙{h→0} r(h)=l$
 Exemple
Exemple
On considère $r(h)={12h+6h^2+h^3}/{h}$
On note $r(h)$ n'est pas défini en 0, ce qui rend la détermination de sa limite difficile.
On simplifie: $r(h)={h(12+6h+h^2)}/{h}=12+6h+h^2$
On note $12+6h+h^2$ est défini en 0, ce qui rend la détermination de sa limite évidente.
On a alors: $\lim↙{h→0}r(h)=12+6×0+0^2=12$
Finalement: $ \lim↙{h→0} r(h)=12$
Définition
Soit $f$ une fonction définie sur un intervalle I. Soit $x_0$ un réel de I.
Soit $h$ un réel tel que $x_0+h$ appartienne à I.
La fonction $f$ est dérivable en $x_0$ si et seulement si il existe un nombre réel $l$ tel que $\lim↙{h→0}{f(x_0+h)-f(x_0)}/{h}=l$.
Ce nombre $l$ s'appelle le nombre dérivé de $f$ en $x_0$. Il se note $f'(x_0)$.
On a alors: $f\,'(x_0)= \lim↙{h→0}{f(x_0+h)-f(x_0)}/{h}$
On note que $f\,'(x_0)$ est la limite du taux d'accroissement de $f$ entre $x_0$ et $x_0+h$ lorsque $h$ tend vers 0.
 Exemple
Exemple
Soit $f$ la fonction définie par $f(x)=x^3$.
Soit $a$ un réel fixé.
Soit $h$ un réel non nul.
Montrer que le taux d'accroissement de $f$ entre $a$ et $a+h$ vaut $3a^2+3ah+h^2$.
Montrer en utilisant la définition du nombre dérivé que $f\,'(a)$ existe et donner son expression.
Que vaut $f'(2)$?
Corrigé
Soit $r(h)$ le taux d'accroissement cherché.
On a: $r(h)={f(a+h)-f(a)}/{h}={(a+h)^3-a^3}/{h}={(a+h)(a^2+2ah+h^2)-a^3}/{h}$
Soit: $r(h)={a^3+2a^2h+ah^2+a^2h+2ah^2+h^3-a^3}/{h}={3a^2h+3ah^2+h^3}/{h}$
Soit: $r(h)={h(3a^2+3ah+h^2)}/{h}$.
$r(h)=3a^2+3ah+h^2$.
On détermine alors si $f\,'(a)$ existe.
C'est le cas si $\lim↙{h→0}r(h)$ existe, et on a alors $f\,'(a)=\lim↙{h→0}r(h)$
On a: $\lim↙{h→0}r(h)=3a^2+3a×0+0^2=3a^2$
Par conséquent, $f\,'(a)$ existe et vaut $3a^2$.
En particulier: $f'(2)=3×2^2=12$
Définition
Soit $f$ une fonction dérivable en $x_0$ et dont la courbe représentative est $C_f$.
La droite passant par $A(x_0; f(x_o))$ et dont le coefficient directeur vaut $f'(x_0)$ s'appelle la tangente à la courbe $C_f$ en $x_0$.
 Exemple
Exemple
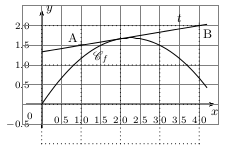
La droite $t$ passe par A(1;1,5) et B(4;2).
$t$ est la tangente à $\C_f$ en 2.
$f$ admet pour maximum $f(2,25)$.
Déterminer graphiquement $f(2)$, $f\,'(2)$ et $f\,'(2,25)$.
Solution...
Corrigé
$f(2)≈1,7$ (c'est l'ordonnée du point de $\C_f$ d'abscisse 2).
$f\,'(2)$ est le coefficient directeur de la tangente $t$ à la courbe $C_f$ en 2.
Or $t$ passe par A et B.
Donc $t$ a pour coefficient directeur ${y_B-y_A}/{x_B-x_A}={2-1,5}/{4-1}={0,5}/{3}={1}/{6}≈0,17$.
Et par là: $f\,'(2)={1}/{6}$.
$f\,'(2,25)$ est le coefficient directeur de la tangente $d$ à la courbe $C_f$ en 2,25.
$d$ n'est pas tracée, mais, comme, $f(2,25)$ est le maximum de $f$,
il est "clair" que $d$ est parallèle à l'axe des abscisses, et par là: $f\,'(2,25)=0$.
En toute rigueur, il faudrait préciser que:
d'une part $2,25$ est à l'intérieur d'un intervalle sur lequel $f$ est dérivable,
d'autre part $f(2,25)$ est le maximum de $f$ sur cet intervalle.
Par conséquent, $f(2,25)$ est un extremum local de $f$,
Et donc: $f\,'(2,25)=0$.
 Exemple
Exemple
Soit $f$ la fonction définie par $f(x)=x^3$.
On a vu précédemment que $f'(2)=12$.
Relier cette valeur au premier exemple du chapitre.
Corrigé
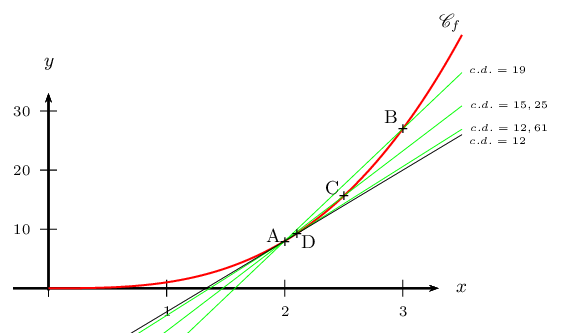
Considérons le premier exemple du chapitre.
Pour $h=1$, ${f(2+h)-f(2)}/{h}$ est le coefficient directeur de la corde (AB), soit 19.
Pour $h=0,5$, ${f(2+h)-f(2)}/{h}$ est le coefficient directeur de la corde (AC), soit 15,25.
Pour $h=0,1$, ${f(2+h)-f(2)}/{h}$ est le coefficient directeur de la corde (AD), soit 12,61.
Quand on passe de B à C, puis de C à D, $h$ se rapproche de 0, et le coefficient directeur de la corde se rapproche de 12.
Or, comme la tangente à $C_f$ en 2 a pour coefficient directeur $f'(2)=12$, on a: $ \lim↙{h→0}{f(2+h)-f(2)}/{h}=12$.
C'est donc cohérent avec les valeurs des coefficients directeurs des cordes qui semblent
de plus en plus proches du coefficient directeur de la tangente à $C_f$ en 2.
A retenir !
Un nombre dérivé est un coefficient directeur de tangente.
Propriété
La tangente à $\C_f$ en $x_0$ a pour équation $y=f(x_0)+f\,'(x_0)(x-x_0)$.
 Exemple
Exemple
On sait que: $f(3)=4$ et que: $f\,'(3)=5$.
Déterminer une équation de la tangente $t$ à $\C_f$ en 3.
Corrigé
Méthode 1
La tangente à $\C_f$ en $x_0$ a pour équation $y=f(x_0)+f\,'(x_0)(x-x_0)$.
ici: $x_0=3$, $f(x_0)=4$, $f\,'(x_0)=5$.
D'où l'équation: $y=4+5(x-3)$, soit: $y=4+5x-15$, soit: $y=5x-11$.
Donc finalement, $t$ a pour équation: $y=5x-11$.
Méthode 2
$f\,'(3)=5$, donc $t$ admet une équation du type: $y=5x+b$.
Or, $f(3)=4$, donc on a: $4=5×3+b$, d'où: $4=15+b$, d'où: $-11=b$.
Donc finalement, $t$ a pour équation: $y=5x-11$.
II. Fonctions dérivées
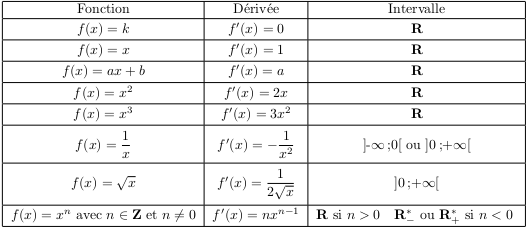
Propriété
Le tableau suivant donne les fonctions de référence, leurs dérivées, et les intervalles sur lesquels sont définies ces dérivées.
Par ailleurs, vous devrez connaître également la dérivée suivante, définie sur $ℝ $.
(cette dérivée concerne une fonction vue dans le chapitre Fonction exponentielle)
La dérivée de $e^x$ est $e^x$.
Opérations
Le tableau ci-contre donne les dérivées d'une somme, d'un produit et d'un quotient de fonctions $u$ et $v$ dérivables sur un même intervalle I (Pour la dérivée du quotient, $v$ est supposée ne pas s'annuler sur I).
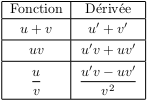
Cas particuliers:
Si $k$ une constante, alors la dérivée de $ku$ est $ku\,'$.
La dérivée de ${1}/{v}$ est ${-v\,'}/{v^2}$.
 Exemple
Exemple
Dériver
- $f(x)=-{5}/{3}x^2-4x+1$,
- $g(x)=3+{1}/{2x+1}$
- $h(x)=(8x+1)√{x}$
- $k(x)={10-x}/{2x}$
Corrigé
Dérivons $f(x)=-{5}/{3}x^2-4x+1$
On pose $k=-{5}/{3}$, $u=x^2$ et $v=-4x+1$.
Donc $u\,'=2x$ et $v\,'=-4$.
Ici $f=ku+v$ et donc $f\,'=ku\,'+v\,'$.
Donc $f\,'(x)=-{5}/{3}2x+(-4)=-{10}/{3}x-4$.
Dérivons $g(x)=3+{1}/{2x+1}$
On pose $v=2x+1$. Donc $v\,'=2$.
Ici $g=3+{1}/{v}$ et donc $g\,'=0+{-v\,'}/{v^2}$.
Donc $g\,'(x)=-{2}/{(2x+1)^2}$.
Dérivons $h(x)=(8x+1)√{x}$
On pose $u=8x+1$ et $v=√{x}$.
Donc $u\,'=8$ et $v\,'={1}/{2√{x}}$.
Ici $h=uv$ et donc $h\,'=u\,'v+uv\,'$.
Donc $h\,'(x)=8√{x}+(8x+1){1}/{2√{x}}=8√{x}+(8x+1)/{2√{x}}$.
Dérivons $k(x)={10-x}/{2x}$
On pose $u=10-x$ et $v=2x$.
Donc $u\,'=-1$ et $v\,'=2$.
Ici $k={u}/{v}$ et donc $k\,'={u\,'v-uv\,'}/{v^2}$.
Donc $k\,'(x)={(-1)2x-(10-x)2}/{(2x)^2}={-2x-20+2x}/{4x^2}={-20}/{4x^2}=-{5}/{x^2}$.
Composée
Soit $a$ et $b$ deux réels fixés.
Soit $g$ une fonction dérivable sur un intervalle I.
Pour tout $x$ tel que $ax+b$ appartienne à I, la fonction $f$ définie par $f(x)=g(ax+b)$ est dérivable,
et on a: $f'(x)=a×g'(ax+b)$
 Exemple
Exemple
Dériver
- $q(x)=(-x+3)^2$
- $n(x)=2√{3x}+(-2x+1)^3$
- $m(x)=e^{-2x+1}$ (cela utilise une fonction vue dans le chapitre Fonction exponentielle)
Corrigé
-
Dérivons $q(x)=(-x+3)^2$
Ici: $q(x)=g(-x+3)$ avec $g(z)=z^2$.
Et donc: $q\,'(x)=-1×g\,'(-x+3)$ avec $g'(z)=2z$.
Donc: $q\,'(x)=-1×2(-x+3)=-2(-x+3)=2x-6$.
Autre méthode: il suffit de développer $q$ avant de dériver.
On a: $q(x)=x^2-6x+9$.
Et donc: $q\,'(x)=2x-6$ -
Dérivons $n(x)=2√{3x}+(-2x+1)^3$
Ici: $√{3x}=g(3x)$ avec $g(z)=√{z}$.
Et donc: $(√{3x})\,'=3×g\,'(3x)$ avec $g'(z)={1}/{2√{z}}$.
Donc: $(√{3x})\,'=3×{1}/{2√{3x}}={3}/{2√{3x}}$.
De même, on a: $(-2x+1)^3=g(-2x+1)$ avec $g(z)=z^3$.
Et donc: $((-2x+1)^3)\,'=-2×g\,'(-2x+1)$ avec $g'(z)=3z^2$.
Donc: $((-2x+1)^3)\,'=-2×3(-2x+1)^2=-6(-2x+1)^2$.
Par conséquent, on obtient:
$n\,'(x)=2 ×{3}/{2√{3x}}+(-6)(-2x+1)^2={3}/{√{3x}}-6(-2x+1)^2$. -
Dérivons $m(x)=e^{-2x+1}$
Ici: $m(x)=g(-2x+1)$ avec $g(z)=e^z$.
Et donc: $m\,'(x)=-2×g\,'(-2x+1)$ avec $g'(z)=e^z$.
Donc: $q\,'(x)=-2×e^{-2x+1}$.