 Fonction exponentielle
Fonction exponentielle
Définition et propriété
Il existe une unique fonction $f$ dérivable sur $\R$ telle que $f\,'=f$ et $f(0)=1$.
C'est la fonction exponentielle. Elle est notée exp.
Le nombre $e$ est l'image de 1 par la fonction exponentielle.
Ainsi $\exp(1)=e$.
A retenir: $e≈2,72$.
Définition et propriété
Pour tout $p$ rationnel, on a $\exp(p)=e^p$.
Par extension, on convient de noter:
pour tout $x$ réel, $\exp(x)=e^x$.
Ainsi exp(0)$=e^0=1$. exp(1)$=e^1=e$.
Dérivées
La fonction $e^x$ admet pour dérivée $e^x$ sur $\R$. Ainsi: $(e^x)'=e^x$
Si $a$ et $b$ sont deux réels fixés, alors la fonction $f$ définie par $f(x)=e^{ax+b}$ est dérivable,
et on a: $f'(x)=a×e^{ax+b}$
 Exemple
Exemple
Dériver chacune des deux fonctions suivantes: $f(x)=3e^x+7x^3+2$. $g(x)=0,5e^{2x-4}$.
Solution...Corrigé
Dérivons $f$.
$f\,'(x)=3e^x+7×3x^2+0=3e^x+21x^2$.
Dérivons $g$.
On pose $a=2$ et $b=-4$.
Ici $g=0,5e^{ax+b}$ et donc $g'=0,5×a×e^{ax+b}$.
Donc $g'(x)=0,5×2×e^{2x-4}=e^{2x-4}$.
Propriétés
La fonction $e^x$ est strictement positive.
La fonction $e^x$ est strictement croissante.
Exemple
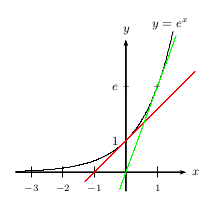
Soit $\C$ la courbe représentative de $e^x$.
Déterminer une équation de $d_0$, tangente à $C$ en 0.
Déterminer une équation de $d_1$, tangente à $C$ en 1.
Corrigé
Posons $f(x)=e^x$. On a donc: $f\,'(x)=e^x$.
$d_0$ a pour équation $y=f(x_0)+f\,'(x_0)(x-x_0)$.
ici: $x_0=0$, $f(x_0)=e^0=1$, $f\,'(x_0)=e^0=1$.
D'où l'équation: $y=1+1(x-0)$, soit: $y=1+x$, soit: $y=x+1$.
Donc finalement, $d_0$ a pour équation: $y=x+1$ (elle est tracée en rouge sur le dessin de la propriété précédente).
$d_1$ a pour équation $y=f(x_0)+f\,'(x_0)(x-x_0)$.
ici: $x_0=1$, $f(x_1)=e^1=e$, $f\,'(x_1)=e^1=e$.
D'où l'équation: $y=e+e(x-1)$, soit: $y=e+ex-e$, soit: $y=ex$.
Donc finalement, $d_1$ a pour équation: $y=ex$ (elle est tracée en vert sur le dessin de la propriété précédente).
 Exemple
Exemple
Quel est le sens de variation de la fonction $f(x)=5e^{2x}+x^3$ sur $\R$?
Solution...Corrigé
Dérivons $f$.
On pose $a=2$ et $b=0$.
Ici $f=5e^{ax+b}+x^3$ et donc $f\,'=5ae^{ax+b}+3x^2$.
Donc $f\,'(x)=5×2×e^{2x}+3x^2=10e^{2x}+3x^2$.
Or, une exponentielle est strictement positive. De plus, un carré est positif. Et enfin, les coefficients 10 et 3 sont strictement positifs.
Par conséquent, $f\,'(x)$ est strictement positif pout tout $x$ réel, et par là, $f$ est strictement croissante sur $\R$.
Propriétés
Pour tous nombres réels $a$ et $b$, $e^{a+b}=e^a×e^b$
${e^a}/{e^b}=e^{a-b}$
Pour tout nombre réel $a$ et entier relatif $b$, $(e^a)^b=e^{ab}$
Exemple
Calculer $s=e^0+e^{0,1}e^{0,9}-3{e^{7,2}}/{e^{6,2}}$ (donner la valeur exacte de $s$, puis une valeur approchée arrondie à 0,1 près)
Solution...Corrigé
$s=1+e^{0,1+0,9}-3e^{7,2-6,2}=1+e^1-3e^1=1-2e^1=1-2e≈-4,4$Remarque:
$e$ s'obtient à la calculatrice en tapant: 2nde ln 1 (pour une TI), ou: SHIFT ln 1 (pour une casio).
Propriétés
Pour tous nombres réels $a$ et $b$, $e^a\text"<"e^b ⇔ a\text"<"b$ et $e^a=e^b⇔a=b$
 Exemple
Exemple
- Résoudre l'équation $e^{x-2}-1=0$.
- Résoudre l'inéquation $e^{-5x+3}-e≤0$.
Corrigé
- Appelons (1) l'équation à résoudre.
$\D_E=\R$.
(1) $⇔$ $e^{x-2}-1=0⇔e^{x-2}=1⇔e^{x-2}=e^0⇔x-2=0⇔x=2$.
Donc $\S_1=\{2\}$. - Appelons (2) l'inéquation à résoudre.
$\D_E=\R$.
(2) $⇔$ $e^{-5x+3}-e≤0$ $⇔$ $e^{-5x+3}≤e$ $⇔$ $e^{-5x+3}≤e^1$ $⇔$ $-5x+3≤1$
Soit: (2) $⇔$ $-5x≤1-3$ $⇔$ $x≥{-2}/{-5}$ $⇔$ $x≥0,4$.
Donc $\S_2=[0,4;+∞[$.
Savoir faire
Le signe d'une expression contenant une exponentielle est souvent évident car une exponentielle est strictement positive.
Quand le signe n'est pas évident, il faut résoudre une inéquation pour savoir quand l'expression est positive (ou négative).
 Exemple
Exemple
- Etudier le signe de $e^{-x-2}+3$.
- Montrer que $e^{-5x+3}(x-2)$>$0$ sur $]2; +∞[$.
- Etudier le signe de $e^{-x}-1$.
Corrigé
-
$e^{-x-2}$>$0$ car une exponentielle est strictement positive.
Donc: $e^{-x-2}+3$>$3$, et par là, $e^{-x-2}+3$ est strictement positive pour tout $x$. -
$e^{-5x+3}$>$0$ car une exponentielle est strictement positive.
Donc le produit $e^{-5x+3}(x-2)$ est du signe de la fonction affine $x-2$.
Or cette dernière s'annule en 2, et son coefficient directeur 1 est strictement positif.
Donc $x-2$>$0$ pour $x$>$2$.
Et par là: $e^{-5x+3}(x-2)$>$0$ sur $]2; +∞[$. -
Cette fois-ci, la positivité de l'exponentielle ne sert à rien, car on lui ôte 1.
Nous allons chercher pour quelles valeurs de $x$ l'expression est positive.
On a: $e^{-x}-1$>$0$ $⇔$ $e^{-x}$>$1$ $⇔$ $e^{-x}$>$e^0$ $⇔$ $-x$>$0$ $⇔$ $x$<$0$.
Donc $e^{-x}-1$>$0$ sur $]-∞;0[$.
Il est alors évident que $e^{-x}-1$<$0$ sur $]0;+∞[$,
et que $e^{-x}-1=0$ pour $x=0$.
Remarque: la propriété qui suit concerne les suites.
Suites $(e^{na})$
Pour tout réel $a$, la suite $(e^{na})$ est une suite géométrique de raison $e^a$ et de premier terme 1.
 Exemple
Exemple
On admet que $1,05≈e^{0,04879}$
La population de bactéries dans un certain bouillon de culture croît de $5\%$ par jour.
Initialement, elle s'élève à $1\,000$ bactéries.
Soit $(u_n)$ le nombre de bactéries au bout de $n$ jours.
Ainsi, $u_0=1\,000$.
Montrer que $u_{n}≈1\,000× e^{0,04879n}$.
Comment qualifier la croissance de la population de bactéries?
Corrigé
Pour tout naturel $n$, on a: $u_{n+1}=1,05u_n$.
Donc $(u_n)$ est géométrique de raison 1,05.
Donc, pour tout naturel $n$, on a: $u_{n}=u_0 ×1,05^n$.
Soit: $u_{n}=1\,000× 1,05^n$.
Or $1,05≈e^{0,04879}$
Donc: $u_{n}≈1\,000× (e^{0,04879})^n$.
Soit: $u_{n}≈1\,000× e^{0,04879n}$.
La population de bactéries suit donc une croissance exponentielle.