Probabilités conditionnelles
Probabilités conditionnelles
Quelques rappels de seconde pour commencer
Propriétés
- Pour tous événements A et B, on a l'égalité: $p(A∪B)=p(A)+p(B)-p(A∩B)$.
- Si A et B sont incompatibles, alors on a l'égalité: $p(A∪B)=p(A)+p(B)$.
- La probabilité d'un événement est la somme des probabilités des événements élémentaires qui le constituent.
- Soit A un événement et $A↖{-}$ son contraire. On a l'égalité : $p(A)+p(A↖{-})=1$.
- Si tous les événements composant l'univers $Ω$ sont équiprobables, alors, pour tout événement A, on obtient:
$p(A)= {\text"nombre d'éléments de A"}/{\text"nombre d'éléments de Ω"}$ On note aussi: $p(A)= {\text"Card A"}/{\text"Card Ω"}$ .
Exemple
On jette 2 dés.
Soit A: "les deux résultats sont inférieurs ou égaux à 4".
Soit B: "la somme des deux résultats vaut 6".
Soit E le contraire de l'événement $A∪B$.
- Modéliser l'expérience pour se placer en situation d'équiprobabilité.
- Déterminer $p(A)$ et $p(B)$.
- Décrire par une phrase chacun des événements: $A∩B$, $A∪B$, $E$
- Déterminer la probabilité de chacun des événements précédents.
- On sait que la somme des deux résultats vaut 6.
Quelle est la probabilité que les deux résultats soient inférieurs ou égaux à 4?
Corrigé
-
Les 36 issues de l'expérience sont décrites par le tableau qui suit.
Nous y avons fait apparaître les sommes des deux dés.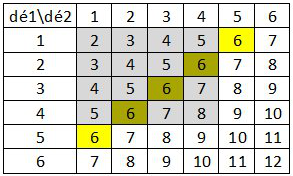
Notons que l'univers aurait aussi pu être décrit par un arbre de dénombrement.
Quelque soit la façon de faire, il y a 36 cas équiprobables. - $\text"Card Ω"=6×6=36$. Il y a équiprobabilité (les 36 cas sont équiprobables).
A est représenté en gris. B est représenté en jaune.
$\text"Card A"=16$. Donc: $p(A)={16}/{36}={4}/{9}≈0,44$.
On remarque que $B$ contient les évènenements 1-5, 2-4, 3-3, 4-2 et 5-1.
$\text"Card B"=5$. Donc: $p(B)={5}/{36}≈0,14$.
- $A∩B$: "les deux résultats sont inférieurs ou égaux à 4 et leur somme vaut 6".
On remarque que $A∩B$ contient les évènenements 2-4, 3-3 et 4-2.
$A∪B$: "les deux résultats sont inférieurs ou égaux à 4 ou leur somme vaut 6".
On remarque $A∪B$ contient $16+(5-3)=16+2=18$ événements.
$E$: " les deux résultats sont strictement supérieurs à 4 et leur somme ne vaut pas 6". - $\text"Card A∩B"=3$. Donc: $p(A∩B)={3}/{36}={1}/{12}≈0,08$.
$p(A∪B)=p(A)+p(B)-p(A∩B)={16}/{36}+{5}/{36}-{3}/{36}={18}/{36}=0,5$.
$p(E)=1-p(A∪B)=1-0,5=0,5$. - On sait que la somme des deux résultats vaut 6.
L'univers se réduit donc aux 5 issues de B, qui sont équiprobables.
Parmi celles-ci, 3 donnent deux résultats inférieurs ou égaux à 4.
Donc la probabilité cherchée est ${3}/{5}=0,6$.
Une remarque évidente: deux événements peuvent avoir la même probabilité sans être identiques!
Voici ci-dessous le cours de première.
Définition
Soit B un événement tel que $p(B)≠0$.
On appelle probabibité conditionnelle de l'événement A sachant B la probabilité notée $p_B(A)$
et définie par l'égalité $p_B(A)={p(A∩B)}/{p(B)}$.
Exemple
On tire 2 jetons successivement et sans remise d'un sac contenant 6 jetons numérotés de 1 à 6.
Soit A: "les deux jetons sont pairs".
Soit B: "le jeton 2 est resté dans le sac".
Quelle est la probabilité que les deux jetons soient pairs sachant que le jeton 2 est resté dans le sac?
Corrigé
On cherche $p_B(A)$.
Déterminons tout d'abord $p(B)$ et $p(A∩B)$.
Les 30 issues de l'expérience sont décrites par le tableau ci-contre.
Comme le premier jeton tiré n'est pas remis, 6 cas sont impossibles; ils sont représentés en noir.
A est représenté en jaune.
B est représenté en gris.
$\text"Card Ω"=6×5=30$.
Il y a équiprobabilité.
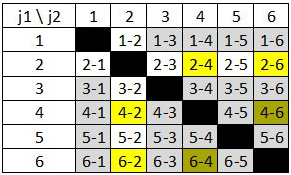
$\text"Card B"=5×4=20$. Donc: $p(B)={20}/{30}={2}/{3}≈0,67$.
$\text"Card A∩B"=2×1=2$. Donc: $p(A∩B)={2}/{30}={1}/{15}≈0,07$.
D'où: $p_B(A)={p(A∩B)}/{p(B)}={{2}/{30}}/{{2}/{3}}={2×3}/{30×2}={1}/{10}=0,1$.
Ce résultat peut se trouver autrement, en raisonnant comme dans l'exemple précédent.
On sait que le jeton 2 est resté dans le sac.
L'univers se réduit donc aux 20 issues de B, qui sont équiprobables.
Parmi celles-ci, 2 donnent deux jetons pairs.
Donc la probabilité cherchée est ${2}/{20}=0,1$.
Probabilité d'une intersection
Soit A un événement tel que $p(A)≠0$.
On a alors l'égalité $p(A∩B)=p(A)×p_A(B)$.
Soit B un événement tel que $p(B)≠0$.
On a alors l'égalité $p(A∩B)=p(B)×p_B(A)$.
Définition et propriété
Soient A et B deux événements.
A et B sont indépendants si et seulement si $p(A∩B)=p(A)×p(B)$
Si $p(A)≠0$, alors: A et B sont indépendants si et seulement si $p(B)=p_A(B)$
Exemple
On tire 1 jeton d'un sac contenant 6 jetons numérotés de 1 à 6.
Soit $A$: "le jeton est pair".
Soit $B$: "le jeton vaut au moins 4".
On a: $A=\{2,4,6\}$ et $B=\{4,5,6\}$ et $A∩B=\{4,6\}$
On obtient: $p(A)={3}/{6}=0,5$, et: $p(B)={3}/{6}=0,5$.
Donc: $p(A)×p(B)=0,5×0,5=0,25$
Or: $p(A∩B)={2}/{6}≈0,33$.
Donc $p(A∩B)≠p(A)×p(B)$
Donc A et B ne sont pas indépendants.
Autre méthode:
On a: $p(B)={3}/{6}$ et $p_A(B)={\text"Card A∩B"}/{\text"Card A"}={2}/{3}$
Donc: $p(B)≠p_A(B)$, et par là: A et B ne sont pas indépendants.
 Exemple
Exemple
On considère une famille de 2 enfants d'âges différents.
En notant F: "l'enfant est une fille", et G: "l'enfant est un garçon", la composition de la famille est dans l'ensemble $Ω=\{(F,F),(F,G),(G,F),(G,G)\}$, chaque couple donnant le sexe de l'ainé, puis celui du cadet.
Les 4 événements sont supposés équiprobables.
Soit A: "les enfants ne sont pas tous de même sexe"
Soit B: "la famille a au plus une fille"
A et B sont-ils indépendants?
Reprendre le problème avec 3 enfants.
Corrigé
On a: $A=\{(F,G),(G,F)\}$, et donc: $p(A)={2}/{4}=0,5$
On a: $B=\{(F,G),(G,F),(G,G)\}$, et donc: $p(B)={3}/{4}=0,75$
On a: $A∩B=A$, et donc: $p(A∩B)=0,5$
On constate que: $p(A)×p(B)=0,5×0,75=0,375$, et par là: $p(A∩B)≠p(A)×p(B)$
Donc A et B ne sont pas indépendants.
Avec 3 enfants, on obtient:
$Ω=\{(F,F,F),(F,F,G),(F,G,F),(F,G,G),(G,F,F),(G,F,G),(G,G,F),(G,G,G)\}$
On a: $A=\{(F,F,G),(F,G,F),(F,G,G),(G,F,F),(G,F,G),(G,G,F)\}$, et donc: $p(A)={6}/{8}=0,75$
On a: $B=\{(F,G,G),(G,F,G),(G,G,F),(G,G,G)\}$, et donc: $p(B)={4}/{8}=0,5$
On a: $A∩B=\{(F,G,G),(G,F,G),(G,G,F)\}$, et donc: $p(A∩B)={3}/{8}=0,375$
On constate que: $p(A)×p(B)=0,75×0,5=0,375$, et par là: $p(A∩B)=p(A)×p(B)$
Donc A et B sont indépendants.
Formule des probabilités totales
Soit $A_1$, $A_2$, ...,$A_n$ $n$ événements constituant une partition de l'univers $Ω$
(c'est à dire que leur réunion est égale à $Ω$, et qu'ils sont disjoints 2 à 2).
Pour tout événement E, on a l'égalité $p(E)=p(A_1∩E)+p(A_2∩E)+...+p(A_n∩E)$.
A retenir
Un arbre de dénombrement permet de comptabiliser le nombre de cas associés à un ou plusieurs événements donnés. Il ne s'utilise que si tous les événements élémentaires sont équiprobables. Aucune probabilité n'y apparaît.
Un arbre de probabilité (ou pondéré) permet de calculer directement la probabilité d'un ou de plusieurs événements donnés. Toutes les branches sont associées à des probabilités.
Propriétés liées aux arbres de probabilités
- règle 1: La somme des probabilités des branches issues d'un même noeud vaut 1.
- règle 2: La probabilité d'un événement associé à une feuille est égale au produit des probabilités des branches du chemin conduisant à la feuille (c'est la généralisation de la formule donnant la probabilité d'une intersection).
- règle 3: La probabilité d'un événement associé à plusieurs feuilles est égale à la somme des probabilités de chacune de ces feuilles (c'est l'application de la formule des probabilités totales).
Exemples
Revenons sur deux exemples précédents, et déterminons certaines réponses en utilisant les arbres pondérés.
Premier exemple
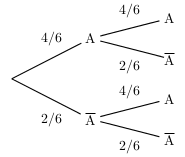
On jette 2 dés.
Soit A: "le résultat est inférieur ou égal à 4".
A-A: "les 2 résultats sont inférieurs ou égaux à 4".
On cherche $p(A-A)$.
On peut dresser l'arbre pondéré ci-contre.
Par application de la seconde règle, on obtient: $p(A-A)={4}/{6}×{4}/{6}={16}/{36}≈0,44$.
Second exemple
On tire 2 jetons successivement et sans remise d'un sac contenant 6 jetons numérotés de 1 à 6.
Soit B: "le jeton tiré n'est pas le jeton 2".
B-B: "aucun des 2 jetons tirés n'est le jeton 2".
On cherche $p(B-B)$.
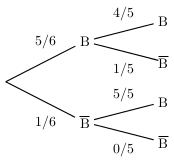
On peut dresser l'arbre de probabilité qui suit.
Par application de la seconde règle, on obtient: $p(B-B)={5}/{6}×{4}/{5}={20}/{30}≈0,67$.
 Exemple
Exemple
On désire évaluer l'efficacité d'un test de dépistage d'une maladie donnée. Le résultat qu'il donne est qualifié de
"positif" ou de "négatif".
15% de la population venant consulter est contaminée.
Si un patient est contaminé, le test est positif 8 fois sur 10.
Et si un patient n'est pas contaminé, le test est tout de même positif 1 fois sur 10 (cela se nomme un faux positif).
Un patient se présente et passe le test.
Soit C: "le patient est contaminé".
Soit S: "le patient est sain".
Soit A: "le test effectué est positif"".
- Quelle est la probabilité que le test soit positif sachant que le patient est contaminé.
- Dresser un arbre pondéré décrivant l'expérience.
- Déterminer la probabilité que le test soit positif et que le patient soit contaminé.
- Déterminer la probabilité que le test soit positif.
- Déterminer la probabilité que le patient soit contaminé sachant que le test est positif.
- Pourquoi peut-on envisager de renoncer à ce test de dépistage?
Corrigé
- La probabilité cherchée est $p_C(A)={8}/{10}=0,8$.
- Arbre pondéré décrivant l'expérience (construit par application de la première règle).
Les probabilités sur les branches de second niveau sont des probabilités conditionnelles!
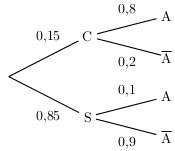
- La probabilité cherchée est $p(C∩A)=p(C)×p_C(A)=0,15×0,8=0,12$ (par application de la seconde règle).
- La probabilité cherchée est $p(A)=p(C∩A)+p(S∩A)$ (par application de la formule des probabilités totales).
Soit: $p(A)=0,12+p(S)×p_S(A)$ (par application de la seconde règle).
Soit: $p(A)=0,12+0,85×0,1=0,12+0,085=0,205$. - La probabilité cherchée est $p_A(C)={p(C∩A)}/{p(A)}={0,12}/{0,205}≈0,59$.
- On peut donc envisager de renoncer à ce test de dépistage. Il n'est pas fiable. En effet, la probabilité qu'un patient soit contaminé sachant que son test est positif est trop faible.
Définition et propriété
Deux épreuves sont indépendantes lorsque le résultat de l'une n'influe pas sur le résultat de l'autre.
Une succession de 2 épreuves indépendantes est telle que, pour tout événement A concernant la première épreuve et pour tout événement B concernant la seconde épreuve, on a:
$p(A∩B)=p(A)×p(B)$
Les événements A et B sont donc indépendants.
Une telle succession peut se représenter par un arbre de probabilité ou un tableau de probabilité.
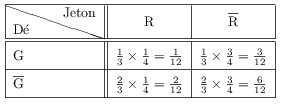
Exemple
On jette un dé, puis on tire un jeton d'un sac contenant les jetons R, V , B et J.
Soit G: "le résultat du dé vaut au moins 5"
Soit R: "le jeton est R"
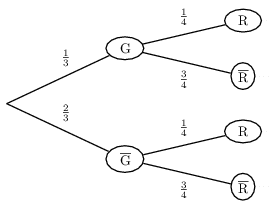
Modéliser l'expérience.
Nous sommes en présence de 2 épreuves indépendantes.
On a: $p(G)={2}/{6}={1}/{3}$ et $p(R)={1}/{4}$
Représentation par un arbre de probabilité.
Représentation par un tableau de probabilité.