 Produit scalaire dans le plan
Produit scalaire dans le plan
L'ensemble des notions de ce chapitre concernent la géométrie plane.
I. Définitions et propriétés
Définition
Soit ${u}↖{→}$ un vecteur, et A et B deux points tels que ${u}↖{→}={AB}↖{→}$.
La norme de ${u}↖{→}$ est la distance AB.
Ainsi: $ ∥{u}↖{→} ∥=AB$.
Définition
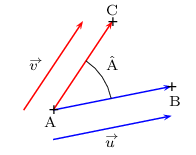
Soient ${u}↖{→}$ et ${v}↖{→}$ deux vecteurs.
Le produit scalaire de ${u}↖{→}$ par ${v}↖{→}$, noté ${u}↖{→}.{v}↖{→}$, est le nombre réel défini de la façon suivante:
Si ${u}↖{→}={0}↖{→}$ ou si ${v}↖{→}={0}↖{→}$, alors ${u}↖{→}.{v}↖{→}=0$
Sinon, si A, B et C sont trois points tels que ${u}↖{→}={AB}↖{→}$ et ${v}↖{→}={AC}↖{→}$,
alors: ${u}↖{→}.{v}↖{→}=∥{u}↖{→} ∥×∥{v}↖{→} ∥×\cos {A}↖{⋏}\,\,\,\,$
Cette dernière égalité s'écrit alors: $${AB}↖{→}.{AC}↖{→}=AB×AC×\cos {A}↖{⋏}\,\,\,\,$$
 Exemple
Exemple
Soient A, B et C trois points tels que $AB=5$, $AC=2$ et ${A}↖{⋏}={π}/{4}$ (en radians).
Calculer le produit scalaire ${AB}↖{→}.{AC}↖{→}$
Corrigé
On a: ${AB}↖{→}.{AC}↖{→}=AB×AC×\cos {A}↖{⋏}$
Soit: ${AB}↖{→}.{AC}↖{→}=5×2×\cos {π}/{4}=10×{√2}/{2}=$$5√2$
Norme et carré scalaire
Soit ${u}↖{→}$ un vecteur. On a alors: $$ ∥{u}↖{→} ∥^2={u}↖{→}.{u}↖{→}\,\,\,\,\,$$
Propriété
Soient ${u}↖{→}$ et ${v}↖{→}$ deux vecteurs non nuls et colinéaires.
Si ${u}↖{→}$ et ${v}↖{→}$ ont même sens, alors $${u}↖{→}.{v}↖{→}=∥{u}↖{→} ∥×∥{v}↖{→} ∥\,\,\,$$
Si ${u}↖{→}$ et ${v}↖{→}$ sont de sens opposés, alors $${u}↖{→}.{v}↖{→}=-∥{u}↖{→} ∥×∥{v}↖{→} ∥\,\,\,$$
 Exemple
Exemple
Soient A, B et C trois points alignés tels que B appartienne au segment $[AC]$ et $AB=4$ et $BC=1$.

Calculer les produits scalaires suivants:
${AB}↖{→}.{AB}↖{→}$ ${AB}↖{→}.{AC}↖{→}$ ${BC}↖{→}.{BA}↖{→}$
Corrigé
${AB}↖{→}.{AB}↖{→}={∥{AB}↖{→} ∥}^2=AB^2=4^2=$$16$
Par ailleurs, comme B appartient au segment $[AC]$, on a: $AC=AB+BC=4+1=5$
et ${AB}↖{→}$ et ${AC}↖{→}$ sont de même sens.
Donc: ${AB}↖{→}.{AC}↖{→}=AB×AC=4×5=$$20$
De même, ${BC}↖{→}$ et ${BA}↖{→}$ sont de sens opposés.
Donc: ${BC}↖{→}.{BA}↖{→}=-BC×BA=-1×4=$$-4$
Propriétés
Soit ${u}↖{→}$, ${v}↖{→}$ et ${w}↖{→}$ trois vecteurs et $λ$ un réel.
Propriété de symétrie: ${u}↖{→}.{v}↖{→}={v}↖{→}.{u}↖{→}$
Propriétés de linéarité: $(λ{u}↖{→}).{v}↖{→}=λ×({u}↖{→}.{v}↖{→})$
${u}↖{→}.({v}↖{→}+{w}↖{→})={u}↖{→}.{v}↖{→}+{u}↖{→}.{w}↖{→}$
 Exemple
Exemple
On sait que ${AD}↖{→}.{AB}↖{→}=5$
On pose: $r=(6{AB}↖{→}).{AC}↖{→}-(2{DC}↖{→}).(3{AB}↖{→})$. Calculer $r$.
Corrigé
On a: $r=6×({AB}↖{→}.{AC}↖{→})-6×({DC}↖{→}.{AB}↖{→})$
Donc: $r=(6{AB}↖{→}).({AC}↖{→}-{DC}↖{→})=(6{AB}↖{→}).({AC}↖{→}+{CD}↖{→})$
Donc: $r=(6{AB}↖{→}).({AD}↖{→})$ (d'après la relation de Chasles)
Donc: $r=6×({AB}↖{→}.{AD}↖{→})$
Soit: $r=6×5$
Soit: $r=30$
Dans ce calcul, de nombreuses parenthèses sont superflues. Elles seront souvent omises par la suite...
Par exemple, on écrira: $r=6{AB}↖{→}.{AC}↖{→}-2{DC}↖{→}.3{AB}↖{→}$
Propriété Produit scalaire et projeté orthogonal
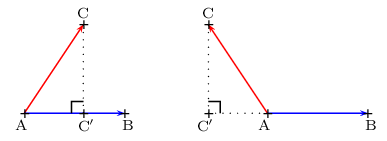
Soient A et B deux points distincts.
Soit C' le projeté orthogonal du point C sur la droite (AB),
Si ${AB}↖{→}$ et ${AC'}↖{→}$ ont même sens, alors $${AB}↖{→}.{AC}↖{→}=AB×AC'\,\,\,$$
Si ${AB}↖{→}$ et ${AC'}↖{→}$ sont de sens opposés, alors $${AB}↖{→}.{AC}↖{→}=-AB×AC'\,\,\,$$
Si ${AC'}↖{→}={0}↖{→}$, alors $${AB}↖{→}.{AC}↖{→}=0\,\,\,$$
 Exemple
Exemple
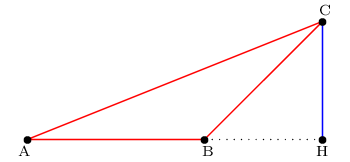
Soit ABC un triangle. Soit H le pied de la hauteur issue de C.
Calculer ${AB}↖{→}.{AC}↖{→}$ si $AH=5$, $AB=3$ et B appartient au segment [AH].
Corrigé
H est le pied de la hauteur issue de C. Or B appartient au segment [AH]. Donc ${AH}↖{→}$ et ${AB}↖{→}$ sont de même sens.
On a donc: ${AB}↖{→}.{AC}↖{→}=AB×AH$
Donc: ${AB}↖{→}.{AC}↖{→}=3×5=15$
Définition et propriété
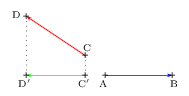
Soient A et B deux points distincts.
Soit C' le projeté orthogonal du point C sur la droite (AB),
Soit D' le projeté orthogonal du point D sur la droite (AB),
On dit alors que le vecteur ${C'D'}↖{→}$ est le projeté orthogonal du vecteur ${CD}↖{→}$ sur le vecteur ${AB}↖{→}$
et on obtient: $${AB}↖{→}.{CD}↖{→}={AB}↖{→}.{C'D'}↖{→}$$
 Exemple
Exemple
Soit ABCD un trapèze rectangle en A et en D tel que $AD=4$, $CD=2$ et $BC={8}/{√{3}}$
Déterminer ${DA}↖{→}.{CB}↖{→}$.
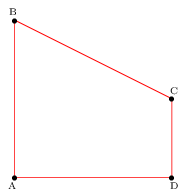
Corrigé
Comme ABCD est un trapèze rectangle en A et en D, il est clair que A et D sont les projetés orthogonaux respectifs de B et C sur la droite (AD).
On obtient alors: ${DA}↖{→}.{CB}↖{→}={DA}↖{→}.{DA}↖{→}$
Soit: ${DA}↖{→}.{CB}↖{→}=DA^2=4^2=16$
Les hypothèses $CD=2$ et $BC={8}/{√{3}}$ sont inutiles pour faire le calcul.
Identités de polarisation Norme et produit scalaire
Soient ${u}↖{→}$ et ${v}↖{→}$ deux vecteurs.
${u}↖{→}.{v}↖{→}={1}/{2}\({∥{u}↖{→}+{v}↖{→}∥}^2-{∥{u}↖{→}∥}^2-{∥{v}↖{→}∥}^2\)\,\,\,\,\,\,\,\,$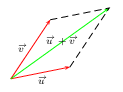
${u}↖{→}.{v}↖{→}={1}/{2}\({∥{u}↖{→}∥}^2+{∥{v}↖{→}∥}^2-{∥{u}↖{→}-{v}↖{→}∥}^2\)\,\,\,\,\,\,\,\,$
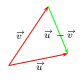
${u}↖{→}.{v}↖{→}={1}/{4}\({{∥{u}↖{→}+{v}↖{→}∥}^2-{∥{u}↖{→}-{v}↖{→}∥}^2\)\,\,\,\,\,\,\,\,$
Applications
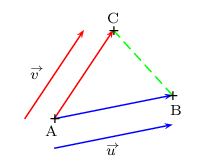
Si ABDC est un parallélogramme tel que ${u}↖{→}={AB}↖{→}$ et ${v}↖{→}={AC}↖{→}$,
alors la première identité devient:
$${AB}↖{→}.{AC}↖{→}={1}/{2}(AD^2-AB^2-AC^2)\,\,\,\,\,$$
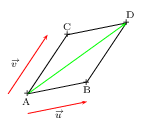
Si A, B et C sont trois points tels que ${u}↖{→}={AB}↖{→}$ et ${v}↖{→}={AC}↖{→}$,
alors la seconde identité devient:
$${AB}↖{→}.{AC}↖{→}={1}/{2}(AB^2+AC^2-BC^2)\,\,\,\,\,$$
 Exemple
Exemple
Soit ABC un triangle tel que $AB=2$, $BC=3$ et $CA=4$
Calculer ${AB}↖{→}.{AC}↖{→}$
Corrigé
${AB}↖{→}.{AC}↖{→}={1}/{2}(AB^2+AC^2-BC^2)={1}/{2}(2^2+4^2-3^2)={1}/{2}(4+16-9)=$$5,5$
La formule qui suit s'obtient très facilement à l'aide de la seconde identité de polarisation.
Formule d'Al-Kashi
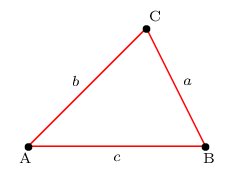
Soit A, B et C trois poins distincts.
On pose: $a=BC$, $b=CA$ et $c=AB$.
La formule d'Al-Kashi est alors la suivante:
$a^2=b^2+c^2-2bc×\cos {A}↖{⋏}$
Cette formule s'appelle aussi Théorème de Pythagore généralisé.
 Exemple
Exemple
Soit ABC un triangle tel que $AB=2$, $BC=3$ et $CA=4$
Déterminer une mesure de l'angle géométrique ${A}↖{⋏}$ (arrondie au degré près).
Corrigé
D'après la formule d'Al-Kashi, on a:
$a^2=b^2+c^2-2bc×\cos {A}↖{⋏}$
Soit: $3^2=4^2+2^2-2×4×2×\cos {A}↖{⋏}$
Et par là: $\cos {A}↖{⋏}={9-16-4}/{-16}={11}/{16}=0,6875$
A l'aide de la calculatrice, on obtient alors une mesure de $ {A}↖{⋏}$, et on trouve: ${A}↖{⋏}≈47°$ (arrondie au degré)
Propriété Produit scalaire et coordonnées
Le plan est muni d'un repère orthonormé $(O,{i}↖{→},{j}↖{→})$.
Soit ${u}↖{→}(x\,;\,y)$ et ${v}↖{→}(x'\,;\,y')$ deux vecteurs.
alors: ${u}↖{→}.{v}↖{→}=xx'+yy'$
Propriété
Le plan est muni d'un repère orthonormé $(O,{i}↖{→},{j}↖{→})$.
Si ${u}↖{→}$ a pour coordonnées $(x\,;\,y)$, alors $$ ∥{u}↖{→} ∥=√{x^2+y^2}\,\,\,$$
 Exemple
Exemple
Le plan est muni d'un repère orthonormé $(O,{i}↖{→},{j}↖{→})$.
Soit ${u}↖{→}(2\,;\,5)$ et ${v}↖{→}(-3\,;\6)$ deux vecteurs.
Quelle est la norme de ${u}↖{→}$?
Calculer ${u}↖{→}.{v}↖{→}$
Corrigé
Le repère est orthonormé. Les calculs qui suivent sont donc valides.
$∥{u}↖{→} ∥=√{x^2+y^2}=√{2^2+5^2}=$$√{29}$
${u}↖{→}.{v}↖{→}=xx'+yy'=2×(-3)+5×6=$$24$
A retenir
Le produit scalaire peut s'exprimer sous 4 formes différentes: à l'aide des normes et d'un angle, en utilisant la projection orthogonale, à l'aide des normes
uniquement, à l'aide des coordonnées.
Mais attention, la formule de calcul analytique du produit scalaire nécessite un repère orthonormal!
Il faut choisir la bonne formule en fonction du problème à résoudre...
II. Applications du produit scalaire
Définition
Deux vecteurs ${u}↖{→}$ et ${v}↖{→}$ sont orthogonaux
si et seulement si ${u}↖{→}.{v}↖{→}=0$.
Propriété
Soit $d$ une droite de vecteur directeur ${u}↖{→}$.
Soit $d'$ une droite de vecteur directeur ${v}↖{→}$.
$d$ et $d'$ sont perpendiculaires si et seulement si ${u}↖{→}.{v}↖{→}=0$.
 Exemple
Exemple
Le plan est muni d'un repère orthonormé $(O,{i}↖{→},{j}↖{→})$.
Soit $A(2\,;\,5)$, $B(1\,;\,3)$ et $C(8\,;\,0)$ trois points.
Les droites (OA) et (BC) sont-elles perpendiculaires?
Corrigé
Le repère est orthonormé. Le calcul de produit scalaire qui suit est donc valide.
On obtient facilement: ${OA}↖{→}(2\,;\,5)$ et ${BC}↖{→}(7\,;\,-3)$
${OA}↖{→}.{BC}↖{→}=xx'+yy'=2×7+5×(-3)=-1$
Donc ${OA}↖{→}.{BC}↖{→}$ n'est pas nul.
Donc les droites (OA) et (BC) ne sont pas perpendiculaires.
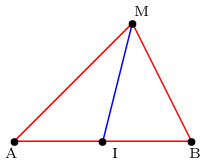
Théorème de la médiane
Soient A et B deux points, et soit I le milieu du segment [AB].
Pour tout point M du plan, on a l'égalité:
${MA}↖{→}.{MB}↖{→}=MI^2-{1}/{4}AB^2$
 Exemple
Exemple
Soient A et B deux points tels que AB=3, et soit I le milieu du segment [AB].
Déterminer l'ensemble $ E$ des points M du plan tels que:
${MA}↖{→}.{MB}↖{→}=11,75$
Corrigé
I est le milieu de [AB].
Donc, d'après le théorème de la médiane, on a:
${MA}↖{→}.{MB}↖{→}=11,75$ $ ⇔$ $MI^2-{1}/{4}AB^2=11,75$ $ ⇔$ $MI^2-{1}/{4}3^2=11,75$
Soit: ${MA}↖{→}.{MB}↖{→}=11,75$ $ ⇔$ $MI^2={9}/{4}+11,75=14$
Soit: ${MA}↖{→}.{MB}↖{→}=11,75$ $ ⇔$ $MI=√{14}$ (car MI est positif)
Donc l'ensemble $ E$ est le cercle de centre I de rayon $√{14}$.
La propriété qui suit s'obtient très facilement à l'aide du théorème de la médiane.
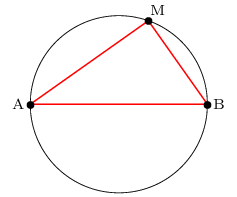
Cercle et produit scalaire
Soient A et B deux points distincts.
L'ensemble des points M du plan tels que ${MA}↖{→}.{MB}↖{→}=0$
est le cercle de diamètre [AB].
Le triangle AMB est rectangle en M si et seulement si M est sur le cercle de diamètre [AB], avec M distinct de A et de B.
 Exemple
Exemple
Soient E, F et G trois points tels que $EF=7$, $FG=11$ et $EG=√{170}$.
Montrer de 2 façons différentes que ${FE}↖{→}.{FG}↖{→}=0$
Que dire du point F?
Corrigé
Méthode 1
On a: $EF^2+FG^2=7^2+11^2=170=EG^2$
Donc le triangle EFG est rectangle en F.
Donc ${FE}↖{→}.{FG}↖{→}=0$
Méthode 2
${FE}↖{→}.{FG}↖{→}={1}/{2}(FE^2+FG^2-EG^2)={1}/{2}(7^2+11^2-(√{170})^2)=0$
Comme ${FE}↖{→}.{FG}↖{→}=0$, le point F est sur le cercle de diamètre [EG].
Savoir faire
Quel est l'intérêt du produit scalaire dans le plan?
Il permet de traiter facilement beaucoup de problèmes où interviennent à la fois les angles (en particulier l'angle droit) et les distances.
Mais, pour chaque problème, il faut choisir la formule adaptée (qui utilise les normes et un angle, ou la projection orthogonale, ou les normes
uniquement, ou les coordonnées)