Fonctions trigonométriques
I. Cercle trigonométrique et radians
Définition
Soit $(O,I,J)$ un repère orthonormal.
Le cercle trigonométrique $\C$ est le cercle de centre O de rayon 1
sur lequel on a choisi comme sens positif de parcours celui qui va de I vers J directement.
Ce sens positif de rotation est appelé sens direct
(en général, il s'agit du sens inverse des aiguilles d'une montre)
Propriétés
Le cercle trigonométrique $\C$ a pour circonférence $2π×1$, soit: $2π$.
Définition et propriété
Lorsque l'on gradue la tangente $d$ en I au cercle trigonométrique $\C$ avec la même unité que le plan (selon le dessin qui suit),
et que l'on enroule la droite des réels obtenue sur $\C$, chaque réel $α$ de $d$ est associé à un unique point M de $\C$.
Si le réel $α$ est dans l'intervalle $[-π;π]$, alors:
le réel $|α|$ est une mesure de l'arc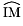 
.
le réel $|α|$ est une mesure en radians de l'angle géométrique
.
Les mesures en radians ainsi obtenues sont dans l'intervalle $[0;π]$; elles sont proportionnelles aux mesures en degrés des angles géométriques.
Exemples
Si le point M est associé au réel $π$ sur le cercle trigonométrique, alors, comme le cercle trigonométrique a pour circonférence $2π$,
l'arc correspond au "demi-tour" du cercle.
Donc une mesure de l'angle géométrique
est $180°$.
A retenir: $π$ radians correspondent à $180°$
Si le point M est associé au réel 1 sur le cercle trigonométrique, alors une mesure de l'arc
est 1, et une mesure de l'angle géométrique
est 1 (en radians).
Et comme les mesures en radians sont proportionnelles aux mesures en degrés, on calcule: $1×{180}/{π}≈57,3$.
Cela correspond donc à un angle géométrique d'environ 57,3°.
A retenir: 1 radian correspond à environ 57,3°
Si le point M est associé au réel $-{π}/{6}$ sur le cercle trigonométrique, alors, comme $|-{π}/{6}|={π}/{6}$,
l'arc 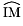mesure ${π}/{6}$, et
l'angle géométrique
mesure ${π}/{6}$ (en radians).
Et comme ${π}/{6}×{180}/{π}=30$, cela correspond à un angle géométrique de 30°
On rappelle que la valeur absolue d'un nombre $a$, notée $|a|$ , est la distance entre les réels $a$ et 0.
Exemple
Donner en radians une mesure de l'angle géométrique
dans chacun des cas suivants.
$=180°$
$=90°$
$=60°$
$=45°$
$=30°$
$=0°$
Corrigé
On a vu que, si $=180°$, alors
une mesure de l'angle géométrique
est $π$.
Et comme les mesures en radians sont proportionnelles aux mesures en degrés, on obtient les résultats suivants.
Quand l'unité de mesure d'un angle n'est pas précisée, il s'agit de radians.
Si $=90°$, alors $={π}/{2}$
Si $=60°$, alors $={π}/{3}$
Si $=45°$, alors $={π}/{4}$
Si $=30°$, alors $={π}/{6}$
Si $=0°$, alors $=0$
Ces valeurs sont à connaître parfaitement....
A retenir !
Radians et degrés sont proportionnels. $π$ radians correspondent à 180 degrés.
Propriétés
Pour tout nombre réel $x$ et pour tout entier relatif $k$,
les réels $x$ et $x+2kπ$ sont associés au même point M sur le cercle trigonométrique.
Deux nombres réels $x$ et $y$ sont associés au même point M sur le cercle trigonométrique si et seulement si il existe un entier relatif $k$ tel que $x-y=2kπ$.
Exemple
Déterminer si $x$ et $y$ sont associés au même point M sur le cercle trigonométrique dans chacun des cas suivants.
1er cas: $x={13π}/{6}$ et $y=-{11π}/{6}$
2ème cas: $x={18π}/{7}$ et $y={31π}/{7}$
Corrigé
1er cas: $x-y={13π}/{6}-(-{11π}/{6})={24π}/{6}=4π=2×2π$
C'est un multiple de $2π$.
Donc $x$ et $y$ sont associés au même point M sur le cercle trigonométrique.
2ème cas: $x-y={18π}/{7}-{31π}/{7}=-{13π}/{7}$. Cela n'est pas un multiple de $2π$. Donc $x$ et $y$ ne sont pas associés au même point M sur le cercle trigonométrique.
II. Fonctions cosinus et sinus
Définition
Pour tout réel $x$, le cosinus de $x$, noté $\cos (x)$, et le sinus de $x$, noté $\sin (x)$, sont les coordonnées du point M associé à $x$ sur le cercle trigonométrique.
Notations: $\cos (x)=\cos x$ $\sin (x)=\sin x$
$(\cos x)^2=\cos^2 x$ $(\sin x)^2=\sin^2 x$
Propriété
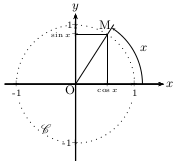
Si OBC est rectangle en B, alors: $\cos O↖{∧}={OB}/{OC}={côté\,adjacent}/{hypoténuse}$
$\sin O↖{∧}={BC}/{OC}={côté\, opposé}/{hypoténuse}$
Cette propriété est cohérente avec la définition précédente pour $|α|$ dans $]0;{π}/{2}[$,
c'est à dire pour un angle géométrique aigu.
On notera que l'écriture proposée confond l'angle $O↖{∧}$ et sa mesure.
Propriétés
Pour tout réel $x$:
$-1≤\cos x≤1$ $-1≤\sin x≤1$ $\cos^2 x+\sin^2 x=1$
Pour tout $k$ entier relatif $\sin (x+2kπ)=\sin x$ $\cos (x+2kπ)=\cos x$
Angles associés
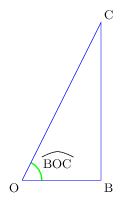
Pour tout réel $α$:
$\cos(-α)=\cos α$ $\sin(-α)=-\sin α$
$\cos(π-α)=-\cos α$ $\sin(π-α)=\sin α$
$\cos(π+α)=-\cos α$ $\sin(π+α)=-\sin α$
$\cos({π}/{2}-α)=\sin α$ $\sin({π}/{2}-α)=\cos α$
Savoir faire
La maîtrise des angles associés est indispensable pour résoudre les équations trigonométriques.
Définition
La fonction sinus est la fonction définie sur $\R$ qui,
à tout réel $x$ associe $\sin x$.
La fonction cosinus est la fonction définie sur $\R$ qui,
à tout réel $x$ associe $\cos x$.
Propriétés
Les fonctions sinus et cosinus sont définies sur $\R$.
Les fonctions sinus et cosinus sont périodiques de période $2π$ sur $\R$.
Par conséquent, pour tout $x$ réel et tout $k$ entier relatif, on a:
$\sin (x+2kπ)=\sin x$
et $\cos (x+2kπ)=\cos x$.
Et par là, dans un repère $(O,i↖{→},j↖{→})$, les courbes représentatives des fonctions sinus et cosinus sont invariantes par toute translation de vecteur
$k2πi↖{→}$.
La fonction sinus est impaire sur $\R$.
Par conséquent, pour tout $x$ réel, $\sin(-x)=-\sin x$.
Et par là, la courbe représentative de la fonction sinus est symétrique par rapport à l'origine.
La fonction cosinus est paire sur $\R$.
Par conséquent, pour tout $x$ réel, $\cos(-x)=\cos x$.
Et par là, dans un repère orthogonal, la courbe représentative de la fonction cosinus est symétrique par rapport à l'axe des ordonnées.
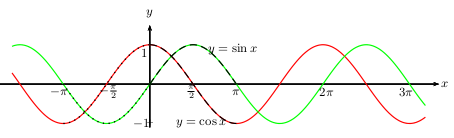
Les fonctions sinus et cosinus vérifient les tableaux de variation ci-dessous.
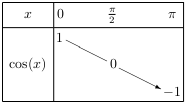
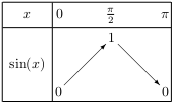
Les fonctions sinus et cosinus vérifient les tableaux de signes ci-dessous.
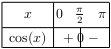
Les fonctions sinus et cosinus vérifient les tableaux de valeurs ci-dessous.
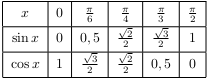
Ces tableaux de valeurs s'étendent à $[0;π]$ en utilisant les angles associés, qui fournissent les égalités: $\sin (π-x)=\sin (x)$ et $\cos (π-x)=-\cos
(x)$.
On obtient chacune des courbes ci-dessous à partir d'un tracé sur $[0;π]$, étendu par symétrie sur $[-π;π]$, et répété à l'infini par translations
successives.
Ces courbes s'appellent des sinusoïdes.
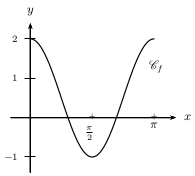
Exemple
Soit $\C_f$ la courbe représentative de la fonction $f$ définie sur $[0;π]$ par $f(x)=\cos^2 x+\cos(2x)$.
Déterminer sans calculatrice les images de $0$, ${π}/{4}$, ${π}/{2}$, ${3π}/{4}$ et $π$.
Tracer l'allure possible de $\C_f$.
Conjecturer le sens de variation de $f$.
Corrigé
Les trois premières images utilisent des valeurs remarquables de cosinus.
$f(0)=(\cos 0)^2+\cos(2×0)=1^2+1=2$
$f({π}/{4})=(\cos {π}/{4})^2+\cos(2×{π}/{4})=({√2}/{2})^2+\cos({π}/{2})={2}/{4}+0=0,5$
$f({π}/{2})=(\cos {π}/{2})^2+\cos(2×{π}/{2})=0^2+\cos(π)=0-1=-1$
Le calcul des l'images suivantes utilisent les angles associés.
$f({3π}/{4})=(\cos {3π}/{4})^2+\cos(2×{3π}/{4})$
Soit: $f({3π}/{4})=(-\cos {π}/{4})^2+\cos({3π}/{2})$
Soit: $f({3π}/{4})=({√2}/{2})^2+0={2}/{4}+0=0,5$
$f(π)=(\cos π)^2+\cos(2×π)=(-1)^2+1=2$
L'allure de $\C_f$, tracé ci-dessous, laisse à penser que $f$ est décroissante sur $[0;{π}/{2}]$, et croissante sur $[{π}/{2};π]$.
Exemple
Voici un exercice technique à la limite du programme...
Résoudre l'équation $\sin x= {√{3}}/{2}$ sur l'intervalle $]-π;π]$.
Résoudre l'équation $\sin x$<$ {√{3}}/{2}$ sur l'intervalle $]-π;π]$.
Les solutions s'obtiennent facilement à l'aide du cercle trigonométrique.
Corrigé
On trace le cercle trigonométrique.
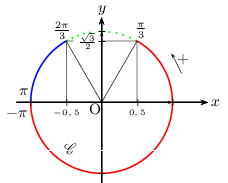
$\sin x= {√{3}}/{2}$ $⇔$ $x={π}/{3}$ ou $x=π-{π}/{3}={2π}/{3}$ ( ces 2 réels sont dans $]-π;π]$ et ce sont les seuls pour sinus ${√{3}}/{2}$)
Donc $S=\{{π}/{3}$;${2π}/{3}\}$
$\sin x$<$ {√{3}}/{2}$ $⇔$ $-π$<$x$<${π}/{3}$ ou ${2π}/{3}$<$x ≤π$
( les réels correspondants sont associés à la zone rouge et à la zone bleue du graphique )
Donc $S=\]-π$;${π}/{3}[\,∪\,]{2π}/{3}$;$π]$