 Suites
Suites
I. Génération et variation d'une suite numérique
Définition
Soit $n_0$ un entier naturel fixé (en général 0 ou 1).
Une suite numérique $(u_n)_{n≥n_0}$ est définie par une relation explicite lorsqu'il existe une fonction $f$
telle que,
pour tout entier $n≥n_0$ , $u_n=f(n)$.
Une suite numérique $(u_n)_{n≥n_0}$ est définie par une relation de récurrence si chaque terme $u_{n+1}$ est fonction du précédent $u_n$ et éventuellement de l'indice $n$.
Une suite peut être définie autrement que par une relation explicite ou par une relation de récurrence.
Exemple
On suppose que:
- Pour tout naturel $n$, $u_n=n^2+3n+1$
- $v_0=10$ et, pour tout naturel $n$, $v_{n+1}=2v_n+3n+2$
- Pour tout naturel $n$, $w_{n}$ est obtenu par l'exécution du programme ci-dessous.

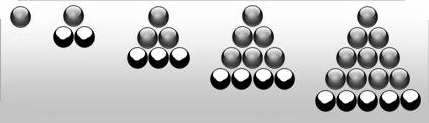
- Pour tout naturel $n$ non nul, $t_{n}$ est le nombre de billes de la figure de rang $n$ obtenue comme ci-dessous.
a. Les suites $(u_n)$, $(v_n)$, $(w_n)$ et $(t_n)$ sont-elles définies de façon explicite, par récurrence, ou autrement?
b. Déterminer $u_{10}$.
c. Déterminer $v_3$.
d. Comment savoir la valeur de $w_2$?
e. Déterminer $t_6$.
f. Définir (sans justifier) la suite $(t_n)$ par une relation de récurrence, puis de façon explicite.
Corrigé
a. La suite $(u_n)$ est définie de façon explicite.
La suite $(v_n)$ est définie par récurrence.
La suite $(w_n)$ est définie par un algorithme; ses valeurs sont des entiers aléatoires entre 1 et 6.
La suite $(t_n)$ est définie par des motifs géométriques.
b. On obtient: $u_{10}=10^2+3×10+1=$$131$
c. On a: $v_0=10$. Et comme: $v_{0+1}=2v_0+3×0+2$, on obtient: $v_1=2×10+2=22$.
De même: $v_{1+1}=2v_1+3×1+2$. Soit: $v_2=2×22+5=49$.
De même: $v_{3}=2v_2+3×2+2=2×49+8=$$106$.
d. La valeur de $w_2$ est un entier aléatoire entre 1 et 6, que l'on ne connait qu'après exécution du programme.
e. On a: $t_1=1$, $t_2=3$, $t_3=6$, $t_4=10$, $t_5=15$.
On obtient facilement: $t_6=15+6=$$21$
f.
On conjecture que:
pour tout entier $n≥1$, $t_{n+1}=t_n+n+1$.
Ceci est bien une relation de récurrence.
On conjecture que:
pour tout entier $n≥1$, $t_{n}=1+2+...+n$.
Ceci est bien une relation explicite.
Pour information, nous verrons ultérieurement que $t_{n}={n(n+1)}/{2}$.
Exemple
On reprend la suite $(v_n)$ de l'exemple précédent, telle que:
$v_0=10$ et, pour tout naturel $n$, $v_{n+1}=2v_n+3n+2$
Ecrire en PYTHON une fonction v(n) qui renvoie la valeur de $v_n$ pour tout naturel $n$
Ecrire en PYTHON une fonction liste(n) qui renvoie la liste des valeurs de $v_0$, $v_1$, $v_2$, ...etc...jusqu'à $v_n$ pour tout naturel $n$
Corrigé
Voici un programme convenable.

La ligne 7, non demandée, permet d'afficher la valeur de $v_3$ dans la console. Il s'y affiche donc 106.
Voici un programme convenable.

La ligne 13, non demandée, permet d'afficher liste des valeurs de $v_0$, $v_1$, $v_2$ et $v_3$ dans la console. Il s'y affiche donc [10, 22, 49, 106]
Sens de variation
Soit $n_0$ un entier naturel fixé (en général 0 ou 1).
La suite $(u_n)_{n≥n_0}$ est croissante si et seulement si pour tout naturel $n≥n_0$: $u_{n+1}≥u_n$.
La suite $(u_n)_{n≥n_0}$ est strictement croissante si et seulement si pour tout naturel $n≥n_0$: $u_{n+1}$>$u_n$.
La suite $(u_n)_{n≥n_0}$ est décroissante si et seulement si pour tout naturel $n≥n_0$: $u_{n+1}≤u_n$.
La suite $(u_n)_{n≥n_0}$ est strictement décroissante si et seulement si pour tout naturel $n≥n_0$: $u_{n+1}$<$u_n$.
La suite $(u_n)_{n≥n_0}$ est constante si et seulement si pour tout naturel $n≥n_0$: $u_{n+1}=u_n$.
 Exemple
Exemple
Déterminer le sens de variation de $(u_n)$ définie par:
$u_0=10$, et pour tout naturel $n$, $u_{n+1}=u_n-n^3-8$
Corrigé
Soit $n$ un entier naturel.
$u_{n+1}-u_n=u_n-n^3-8-u_n=-n^3-8$.
Or, comme $n$ est un entier naturel, il est positif, et par là: $n^3≥0$
Et donc: $-n^3-8≤-0-8$
Et par là: $u_{n+1}-u_n$<$0$.
Et donc: $u_{n+1}$<$u_n$.
Et c'est vrai pour tout naturel $n$.
Donc la suite $(u_n)$ est strictement décroissante.
Propriété
Soit $n_0$ un entier naturel fixé (en général 0 ou 1).
Si $f$ est une fonction monotone sur $[n_0;+ ∞[$, alors la suite $(u_n)_{n≥n_0}$ définie par la relation explicite $u_{n}=f(n)$ a même sens de variation que $f$.
 Exemple
Exemple
Déterminer le sens de variation de $(u_n)$ définie, pour tout naturel $n$, par:
$u_{n}=n^2$
Corrigé
On a ici $u_n=f(n)$ avec $f(x)=x^2$.
Or la fonction $f$ est strictement croissante sur $[0;+ ∞[$.
Donc la suite $(u_n)$ est également strictement croissante.
 Exemple
Exemple
Déterminer le sens de variation de $(u_n)$ définie, pour tout naturel $n$ non nul, par:
$u_{n}=n2^n$
Corrigé
On a ici $u_n=f(n)$ avec $f(x)=x2^x$.
Mais le sens de variation de $f$ n'est pas connu.
On peut alors songer alors à étudier le signe de $u_{n+1}-u_n$.
Mais ici, une autre méthode est possible.
Comme tous les termes sont strictement positifs, nous allons comparer ${u_{n+1}}/{u_n}$ à 1.
On a: ${u_{n+1}}/{u_n}={(n+1)2^{n+1}}/{n2^n}={n+1}/{n}×2=({n}/{n}+{1}/{n})×2=(1+{1}/{n})×2$
Or $1+{1}/{n}$>$1$ et $2$>$1$. Donc: ${u_{n+1}}/{u_n}$>$1$.
Et donc: $u_{n+1}$>$u_n$ (la stricte positivité de $u_n$ conserve le sens de l'inégalité).
Et c'est vrai pour tout naturel $n$.
Donc la suite $(u_n)$ est strictement croissante.
II. Suites arithmétiques et suites géométriques
Définition
Une suite $(u_n)$ est arithmétique de raison $a$ si et seulement si
pour tout naturel $n$, $u_{n+1}=u_n+a$.
(ici, la suite est donnée par une formule de récurrence)
Propriété
$(u_n)$ est arithmétique de raison $a$ si et seulement si
pour tout naturel $n$, $u_{n}=u_0+na$.
(ici, la suite est donnée par une formule explicite)
Propriété
Une suite $(u_n)$ de premier terme $u_0$ est arithmétique de raison $a$ si et seulement si elle est représentée par des points alignés sur la droite d'équation
$y=ax+u_0$.
Propriété
Soit $(u_n)$ une suite arithmétique de raison $a$.
$(u_n)$ est strictement croissante si et seulement si $a$>$0$.
$(u_n)$ est strictement décroissante si et seulement si $a$<$0$.
$(u_n)$ est constante si et seulement si $a=0$.
Propriété
Pour tout naturel $n$, $1+2+3+...+n={n(n+1)}/{2}$.
 Exemple
Exemple
Un loyer annuel de $5\,000$ euros est augmenté de 51 euros chaque année.
Soit $u_n$ le loyer (en euros) la $n+1$ième année. Ainsi, $u_0=5\,000$.
a. Exprimer $u_{n+1}$ en fonction de $u_n$ pour tout naturel $n$.
b. Qu'en déduire concernant la nature de la suite $(u_n)$?
c. Quel est le sens de variation de $(u_n)$?
d. Exprimer $u_{n}$ en fonction de $n$ .
e. Déterminer la somme des loyers des 10 premières années .
Corrigé
a. $u_{n+1}=u_n+51$ pour tout naturel $n$.
b. Par conséquent, la suite $(u_n)$ est arithmétique de raison $a=51$
c. Comme la suite arithmétique $(u_n)$ a une raison strictement positive, elle est strictement croissante.
d. Par ailleurs, comme la suite arithmétique $(u_n)$ est de raison $a$, on obtient: $u_{n}=u_0+na$.
Soit: $u_{n}=5\,000+51n$.
e. Soit $S_a$ la somme des loyers des 10 premières années .
On a: $S_a=u_0+u_1+u_2+...+u_9$
Soit: $S_a=5\,000+(5\,000+51)+(5\,000+51×2)+...+(5\,000+51×9)$
Soit: $S_a=5\,000×10+51(1+2+...+9)$
Soit: $S_a=50\,000+51×{9×10}/{2}$
Soit: $S_a=52\,295$
La somme des loyers des 10 premières années s'élève à $52\,295$ euros.
Définition
Une suite $(u_n)$ est géométrique de raison $q$ si et seulement si
pour tout naturel $n$, $u_{n+1}=u_n× q$.
(ici, la suite est donnée par une formule de récurrence)
Propriété
$(u_n)$ est géométrique de raison $q$ si et seulement si
pour tout naturel $n$, $u_{n}=u_0× q^n$.
(ici, la suite est donnée par une formule explicite)
Propriété
Soit $(v_n)$ une suite géométrique de raison $q$.
$(q^n)$ est strictement croissante si et seulement si $q$>$1$.
$(q^n)$ est strictement décroissante si et seulement si $0$<$q$<$1$.
Si $v_0$>$0$, alors $(v_n)$ et $(q^n)$ ont même sens de variation.
Si $v_0$<$0$, alors $(v_n)$ et $(q^n)$ ont des sens de variation opposés.
Propriété
Soit $q$ un réel différent de1.
Pour tout naturel $n$, $1+q+q^2+q^3+...+q^n={1-q^{n+1}}/{1-q}$.
 Exemple
Exemple
Un loyer annuel de de $4\,700$ euros est augmenté de $2%$ chaque année.
Soit $v_n$ le loyer (en euros) la $n+1$ième année. Ainsi, $v_0=5\,000$.
a. Exprimer $v_{n+1}$ en fonction de $v_n$ pour tout naturel $n$.
b. Qu'en déduire concernant la nature de la suite $(v_n)$?
c. Quel est le sens de variation de $(v_n)$?
d. Exprimer $v_{n}$ en fonction de $n$ .
d. Déterminer la somme des loyers des 10 premières années .
Corrigé
a. Pour tout naturel $n$, on a: $v_{n+1}=v_n(1+{2}/{100})$ .
Soit: $v_{n+1}=1,02v_nn$ .
b. Par conséquent, la suite $(v_n)$ est géométrique de raison $q=1,02$
c. Comme la suite géométrique $(v_n)$ a une raison strictement supérieure à 1, et que $v_0$>$0$, elle est strictement croissante.
d. Par ailleurs, comme la suite géomérique $(v_n)$ est de raison $q$, on obtient: $v_{n}=v_0×q^n$.
Soit: $v_{n}=4\,700×1,02^n$.
e. Soit $S_g$ la somme des loyers des 10 premières années .
On a: $S_g=v_0+v_1+v_2+...+v_9$
Soit: $S_g=4\,700+4\,700×1,02+4\,700×1,02^2+...+4\,700×1,02^9$
Soit: $S_g=4\,700×(1+1,02+1,02^2+...+1,02^9)$
Soit: $S_g=4\,700×{1-1,02^{10}}/{1-1,02}$
Soit: $S_g≈51\,464$
La somme des loyers des 10 premières années s'élève à environ $51\,464$ euros.
 Exemple
Exemple
Représenter chacune des suites $(u_n)$ et $(v_n)$ des exemples précédents.
En déduire graphiquement le plus petit naturel $n$ pour lequel $v_n$>$u_n$.
Corrigé
La suite $(u_n)$ de premier terme $u_0=5\,000$ est arithmétique de raison $a=60$.
Elle est donc représentée par des points (en vert) alignés sur la droite d'équation $y=60x+5\,000$.
Pour représenter (en rouge) les premiers termes de $(v_n)$, il suffit de les calculer grace à la formule $v_{n}=4\,700×1,02^n$.
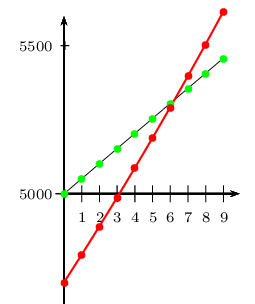
Graphiquement, on constate que l'entier cherché est $n=7$
Savoir faire
Pour montrer qu'une suite $(u_n)$ est géométrique de raison $q$, on essaie en général de prouver la relation de récurrence $u_{n+1}=u_n× q$.
Mais, si cela semble difficile, on essaie alors de prouver la relation explicite $u_{n}=u_0× q^n$.
Quelle que soit la méthode, les relations doivent être vérifiées pour tout naturel $n$.
Il ne faut pas se contenter de faire quelques vérifications avec des valeurs de $n$ particulières!
A retenir
Une augmentation régulière de $a$ est associée à une suite arithmétique de raison $a$.
Une augmentation régulière de $t\%$ est associée à une suite géométrique de raison $1+t\%$.
Une baisse régulière de $t\%$ est associée à une suite géométrique de raison $1-t\%$.
III. Suites et limites
Limite infinie
La suite $(u_n)$ a pour limite $+∞$ quand $n$ tend vers $+∞$ lorsque
tout intervalle du type $[A;+∞[$ (où $A$ est un réel) contient tous les termes $u_n$
de la suite à partir d'un certain rang.
Cela signifie que les $u_n$ deviennent aussi grands que l'on veut pourvu que $n$ soit assez grand.
On note $\lim↙{n→+∞}u_n=+∞$.
La suite $(u_n)$ a pour limite $-∞$ quand $n$ tend vers $+∞$ lorsque
tout intervalle du type $]-∞;A]$ (où $A$ est un réel) contient tous les termes $u_n$
de la suite à partir d'un certain rang.
On note $\lim↙{n→+∞}u_n=-∞$.
Exemple
Soit $u$ la suite définie par $u_n=3n^2-5$ pour tout naturel $n$.
Repprésenter graphiquement $(u_n)$ pour $n$ entre 0 et 5.
Soit $A=30$. Déterminer graphiquement $n_A$, plus petit naturel à partir duquel l'intervalle $[A;+∞[$ contient tous les termes $u_n$.
Conjecturer la valeur de $\lim↙{n→+∞}u_n$.
Démontrer la conjecture.
Corrigé
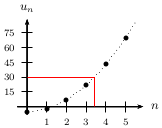
Graphiquement, on note que, pour A=30, $n_A=4$.
A partir de $n=4$, tous les $u_n$ sont supérieurs à $30$.
On conjecture que: $\lim↙{n→+∞}u_n=+∞$.
La démonstration qui suit, à la limite du programme, est réservée aux experts!
On va montrer que tout intervalle du type $[A;+∞[$ (où $A$ est un réel) contient tous les termes $u_n$
de la suite à partir d'un certain rang.
On note que: $u_n≥A$ $ ⇔$ $3n^2-5≥A$ $⇔$ $n^2≥{A+5}/{3}$
Si $A≤-5$ alors l'inégalité précédente est vraie pour tout naturel $n≥n_0$, où $n_0=0$ (car un carré est positif ou nul).
Si $A>-5$ alors on obtient: $u_n≥A$ $ ⇔$ $n≥√ {{A+5}/{3}}$
Et par là, si $n_0$ est le plus petit naturel supérieur ou égal à $√ {{A+5}/{3}}$, alors l'inégalité précédente est vraie pour tout naturel $n≥n_0$
Finalement, tout intervalle du type $[A;+∞[$ contient tous les termes $u_n$
de la suite à partir d'un certain rang $n_0$.
Cela prouve que $\lim↙{n→+∞}u_n=+∞$
Limite finie
La suite $(u_n)$ a pour limite $l$ quand $n$ tend vers $+∞$ lorsque
tout intervalle ouvert contenant $l$ contient tous les termes $u_n$
de la suite à partir d'un certain rang.
Cela signifie que l'on les $u_n$ deviennent aussi proches de $l$ que l'on veut pourvu que $n$ soit assez grand.
On note $\lim↙{n→+∞}u_n=l$.
On dit que la suite converge vers $l$.
Exemple
Soit $(u_n)$ la suite définie par $u_n=3+{1}/{n}$ pour tout naturel $n$ non nul.
A l'aide de votre calculatrice, conjecturer la valeur de $\lim↙{n→+∞}u_n$.
Corrigé
On calcule $u_1=4$, $u_{10}=3,1$, $u_{100}=3,01$ et $u_{1000}=3,001$.
On conjecture alors que: $\lim↙{n→+∞}u_n=3$.
 Exemple
Exemple
Une somme de 1000 euros est placée à intérêts composés au taux de 0,2% par mois.
Soit $(u_n)$ le capital disponible au bout de $n$ mois.
- Exprimer $u_{n+1}$ en fonction de $u_n$ pour tout entier naturel $n$.
En déduire la nature de $(u_n)$.
Donner alors une formule explicite donnant $u_n$ en fonction de $n$ pour tout entier naturel $n$. - On admet que $\lim↙{n→+∞}u_n$ existe. Conjecturer la valeur de $\lim↙{n→+∞}u_n$.
- Donner le sens de variation de $(u_n)$.
-
Soit A un nombre donné quelconque. Il existe une valeur de $n$ à partir de laquelle tous les termes $u_n$ sont supérieurs à A. Pourquoi?
Ecrire l'algorithme d'un programme permettant de trouver le plus petit rang $n_0$ à partir duquel $u_n$ est supérieur à un nombre A donné.
Ecrire en PYTHON un programme convenable.
Qu'affiche un tel programme pour A=2000?
Pourquoi votre algorithme fournit-il effectivement le plus petit $n_0$ convenable?
Corrigé
- $u_{n+1}=u_n+{0,2}/{100}u_n=(1+0,002)u_n=1,002u_n$ (pour tout entier naturel $n$).
Donc $(u_n)$ est géométrique de raison 1,002.
Donc $u_n=1,002^nu_0=$$1,002^n×1000$ (pour tout entier naturel $n$). - On conjecture (à l'aide de la calculatrice) que: $\lim↙{n→+∞}u_n=+∞$.
- $1,002\text">"1$, donc $(1,002^n)$ est strictement croissante.
Et comme 1000>0, $(1,002^n×1000)$ est strictement croissante.
Donc $(u_n)$ est strictement croissante. - Il existe une valeur de $n$ à partir de laquelle tous les termes $u_n$ sont supérieurs à A car $\lim↙{n→+∞}u_n=+∞$.
Un algorithme convenable:
ENTREE
Lire A
INITIALISATION
Affecter à N la valeur 0
Affecter à U la valeur 1000
TRAITEMENT
Tant que U$≤$A
Affecter à U la valeur Ux1,002
Affecter à N la valeur N+1
Fin du Tant que
SORTIE
Afficher N
Voici un programme convenable.

Pour A=2000, il s'affiche 347 (c'est la valeur de $n_0$).
Le programme fournit effectivement le plus petit $n_0$ convenable car $(u_n)$ est croissante.