Polynômes du second degré
Polynômes du second degré
PARTIE 1 (aspect algébrique)
Cette partie est traitée en début d'année de première. Elle suffit pour traiter tous les exercices de ce chapitre.Définition
Un polynôme du second degré (ou trinôme du second degré, ou trinôme) est une fonction $f$ définie sur $\R$ par une expression du type: $f(x)=ax^2+bx+c$ où $a$, $b$ et $c$ sont des nombres réels avec $a≠0$.
$a$ est le coefficient d'ordre 2 du trinôme (on dit aussi coefficient dominant du trinôme).
$b$ est le coefficient d'ordre 1 du trinôme.
$c$ est le coefficient d'ordre 0 du trinôme.
Exemple
Parmi les fonctions suivantes, lequelles sont des polynôme du second degré?
$f(x)=-x^2+x+3$ $g(x)=x^3+x$ $h(x)=x^2$ $l(x)=-3x+1$
Corrigé
$f$ est un trinôme du second degré avec $a=-1$, $b=1$ et $c=3$.
$g$ n'est pas un polynôme du second degré (c'est un polynôme du troisième degré).
$h$ est polynôme du second degré avec $a=1$, $b=0$ et $c=0$.
$l$ n'est pas un polynôme du second degré (c'est une fonction affine).
Propriété
Tout polynôme du second degré $ax^2+bx+c$ peut s'écrire sous la forme $a(x-α)^2+β $,
où $α$ et $β $ sont des réels fixés.
Cette écriture est la forme canonique du trinôme.
On notera que $α={-b}/{2a}$ et que $β$ est l'image de $α$ par le trinôme.
Réciproquement, toute fonction du type $a(x-α)^2+β$ (avec $a≠0$) est un polynôme du second degré.
Exemple
On considère le trinôme $f(x)=2x^2+12x+8$
Montrer que $f$ admet pour forme canonique $2(x+3)^2-10$
En déduire l'extremum de $f$.
Corrigé
La forme proposée est convenable (avec $α=-3$ et $β=-10$).
On veut donc montrer que $f(x)=2(x+3)^2-10$
On développe le second membre.
On obtient: $2(x+3)^2-10=2(x^2+2×x×3+3^2)-10$
Soit: $2(x+3)^2-10=2(x^2+6x+9)-10$
Soit: $2(x+3)^2-10=2x^2+12x+18-10$
Soit: $2(x+3)^2-10=2x^2+12x+8$
Soit: $2(x+3)^2-10=f(x)$.
Donc $f$ admet bien pour forme canonique $2(x+3)^2-10$
On voit que $f(-3)=-10$.
Par ailleurs, comme un carré est positif ou nul, on obtient: $(x+3)^2≥0$, et donc: $2(x+3)^2-10≥2×0-10$.
Donc finalement: $f(x)≥f(-3)$, et c'est vrai pour tout $x$.
Donc $f$ admet pour minimum $-10$ (et ce minimum est atteint pour $x=-3$).
Savoir faire
La forme canonique peut s'obtenir par la méthode de complétion du carré.
On utilise alors l'identité $x^2-2αx=(x-α)^2-α^2$.
Exemple
On considère le trinôme $f(x)=x^2+8x-5$
Ecrire $f$ sous forme canonique par la méthode de complétion du carré
Résoudre $f(x)=-12$.
Résoudre $f(x)$<$-12$.
Résoudre $f(x)$>$-12$.
Corrigé
On a: $f(x)=x^2+8x-5=x^2+2×x×4-5$
Soit: $f(x)=x^2+8x-5=x^2+2×x×4+4^2-4^2-5$
Soit: $f(x)=x^2+8x-5=(x+4)^2-16-5$
Soit: $f(x)=x^2+8x-5=(x+4)^2-21$
Donc $f$ admet pour forme canonique $(x+4)^2-21$
On note que le coefficient dominant est $a=1$; il est implicitement devant le carré.
On peut vérifier que ${-b}/{2a}={-8}/{2}=-4=α$
On a: $f(x)=-12$ $⇔$ $(x+4)^2-21=-12$ $⇔$ $(x+4)^2=9$
Soit: $f(x)=-12$ $⇔$ $x+4=-3$ ou $x+4=3$
Soit: $f(x)=-12$ $⇔$ $x-7$ ou $x=-1$
Donc S$=\{-7;-1\}$
On a: $f(x)$<$-12$ $⇔$ $(x+4)^2-21$<$-12$ $⇔$ $(x+4)^2$<$9$
Soit: $f(x)$<$-12$ $⇔$ $-3$<$x+4$<$3$
Soit: $f(x)$<$-12$ $⇔$ $-7$<$x$<$-1$
Donc S$=]-7;-1[$
De même, on a: $f(x)$>$-12$ $⇔$ $(x+4)^2$>$9$
Soit: $f(x)=-12$ $⇔$ $x+4$<$-3$ ou $x+4$>$3$
Soit: $f(x)=-12$ $⇔$ $x$<$-7$ ou $x$>$-1$
Donc S$=]-\∞;-7[∪]-1;+\∞[$
A retenir
La forme canonique est pratique pour déterminer l'extremum du trinôme, ou pour résoudre rapidement certaines équations ou inéquations.
Définition
Le polynôme du second degré $ax^2+bx+c$ admet pour discriminant le réel $Δ=b^2-4ac$.
Propriété
Soit $ax^2+bx+c$ un trinôme de discriminant $Δ$.
Si $Δ$<$0$, alors le trinôme n'a pas de racine, et son signe reste constant.
Si $Δ=0$, alors le trinôme a une racine unique (dite "double") $x_0={-b}/{2a }$.
Si $Δ$>$0$, alors le trinôme a exactement 2 racines $x_1={-b-√{Δ}}/{2a }$ et $x_2={-b+√{Δ}}/{2a }$.
Exemple
Résoudre l'équation $3x^2+12x+8=0$
Corrigé
$3x^2+12x+8=0$ est un trinôme avec $a=3$, $b=12$ et $c=8$.
$Δ=b^2-4ac=12^2-4×3×8=48$.
$Δ>0$. Le trinôme a 2 racines
$x_1={-b-√Δ}/{2a}={-12-√{48}}/{2×3}=-{6+2√{3}}/{3}≈-3,15$
et $x_2={-b+√Δ}/{2a}={-12+√{48}}/{2×3}={-6+2√{3}}/{3}≈-0,85$.
Donc S$=\{-{6+2√{3}}/{3};{-6+2√{3}}/{3} \}$
Propriété
Soit $ax^2+bx+c$ un trinôme de discriminant $Δ$.
Si $Δ$<$0$, alors le trinôme n'admet pas de forme factorisée dans $\R$.
Si $Δ=0$, alors le trinôme de racine $x_0$ s'écrit sous forme factorisée $a(x-x_0)^2$.
Si $Δ$>$0$, alors le trinôme de racines $x_1$ et $x_2$ s'écrit sous forme factorisée $a(x-x_1)(x-x_2)$.
Toute fonction du type $a(x-x_1)(x-x_2)$ (où $a≠0$, et où $x_1$ et $x_2$ sont 2 réels éventuellement confondus) est un polynôme du second degré
Exemple
On considère le trinôme $f(x)=3x^2+12x+8$
Ecrire, si possible, $f$ sous forme factorisée.
Dresser le tableau de signes de $f$.
Corrigé
On a vu dans l'exemple précédent que ce trinôme (de coefficient dominant $a=3$) a 2 racines
$x_1=-{6+2√{3}}/{3}$ et $x_2={-6+2√{3}}/{3}$.
Donc il est factorisable, et on obtient: $f(x)=3(x+{6+2√{3}}/{3})(x-{-6+2√{3}}/{3})$
Voici alors le tableau de signes de $f$.

A retenir
La forme factorisée est pratique pour résoudre certaines équations ou inéquations, ou pour étudier le signe du trinôme.
Propriété
Soit $ax^2+bx+c$ un trinôme admettant 2 racines éventuellement confondues.
Soit $p$ le produit de ces racines, et $s$ leur somme.
On a alors: $p={c}/{a}$ et $s={-b}/{a}$.
Exemple
On considère le trinôme $f(x)=-5x^2-12x-7$
Ce trinôme possède une racine évidente. Laquelle?
Déterminer le produit des racines de $f$.
En déduire la seconde racine de $f$.
Corrigé
$f$ est un trinôme avec $a=-5$, $b=-12$ et $c=-7$.
Il est évident que $f(-1)=0$.
Donc $-1$ est une racine de $f$.
Le produit des racines de $f$ vaut ${c}/{a}={-7}/{-5}=1,4$.
Donc la seconde racine vaut ${1,4}/{-1}=-1,4$
PARTIE 2 (aspect analytique et géométrique)
Cette partie est traitée après les leçons sur la dérivation et la géométrie repérée.C'est pourquoi les corrigés des exercices de ce chapitre sont rédigés sans nécessairement en utiliser les propriétés.
Propriété
Soit $p(x)=ax^2+bx+c$ un trinôme du second degré.
Sa forme canonique $a(x-α)^2+β $ est telle que $α={-b}/{2a}$ et $β=p(α)$.
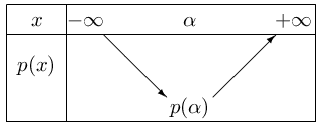
Si $a$>$0$, alors $p$ admet le tableau de variations suivant:
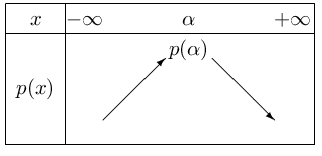
Si $a$<$0$, alors $p$ admet le tableau de variations suivant:
Propriété
Soit $p(x)=ax^2+bx+c$ un trinôme du second degré.
Si $p$ n'a pas de racines, alors il reste du signe de $a$ sur $\R$.
Si $p$ a une racine double $x_0$, alors il est nul en $x_0$, et il est du signe de $a$ ailleurs.
Si $p$ a deux racines distinctes $x_1$ et $x_2$, alors il est nul en $x_1$ et en $x_2$,
il est du signe de $a$ à l'extérieur de ses racines, et il est du signe opposé à celui de $a$ entre ses racines.
Propriété
Soit $p(x)=ax^2+bx+c$ un trinôme du second degré.
Sa représentation graphique dans un repère orthonormé est une parabole dont le sommet a pour coordonnées $(α;β)$, avec $α={-b}/{2a}$ et
$β=p(α)$.
Cette parabole admet l'axe d'équation $x=α$ pour axe de symétrie.
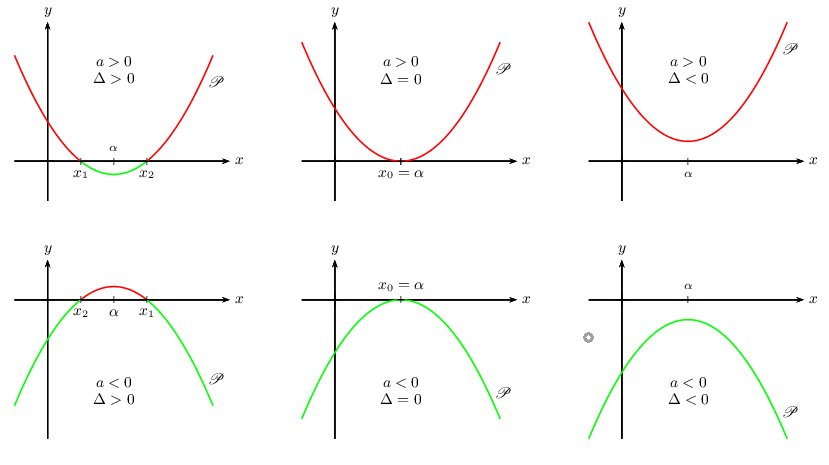
Ci-dessous une synthèse graphique donnant les différentes positions de la parabole représentant un polynôme du second degré.
Le sens de variation, les racines éventuelles et le signe sont alors évidents.