Variations
Variations
Sens de variation
Soit I un intervalle.
$f\,'=0$ sur I si et seulement si $f$ est constante sur I.
$f\,'≥0$ sur I si et seulement si $f$ est croissante sur I.
$f\,'>0$ presque partout sur I si et seulement si $f$ est strictement croissante sur I.
$f\,'≤0$ sur I si et seulement si $f$ est décroissante sur I.
$f\,'$<$0$ presque partout sur I si et seulement si $f$ est strictement décroissante sur I.
 Exemple
Exemple
$f(x)=x^3+x^2-5x+3$ sur $\R$. Déterminer le sens de variation de $f$ sur $\R$.
Solution...Corrigé
Il suffit de calculer $f\,'(x)$, de trouver son signe, et d'en déduire le sens de variation de $f$.
$f\,'(x)=3x^2+2x-5$.
$f\,'$ est un trinôme avec $a=3$, $b=2$ et $c=-5$.
$Δ=b^2-4ac=2^2-4×3×(-5)=64$.
$Δ>0$. Le trinôme a 2 racines $x_1={-b-√Δ}/{2a}={-2-8}/{6}=-{5}/{3}$ et $x_2={-b+√Δ}/{2a}={-2+8}/{6}=1$.
méthode 1
On factorise le trinôme.
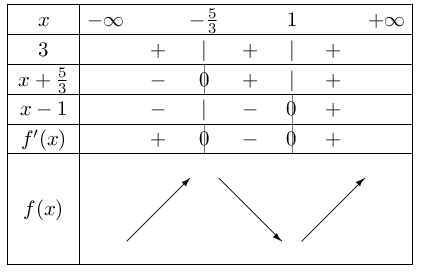
$f\,'(x)=3(x+{5}/{3})(x-1)$.
D'où le tableau suivant:
méthode 2
A utiliser si on connait la seconde partie du cours sur les trinômes.
Comme $a$>$0$, on obtient directement le tableau suivant:
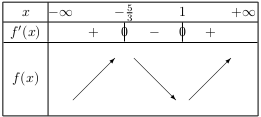
Savoir faire
A quoi peut servir la dérivée d'une fonction?
La valeur de la dérivée en un point permet d'y déterminer le coefficient directeur de la tangente à la courbe de la fonction en ce point.
Le signe de la dérivé sur un intervalle permet de déterminer le sens de variation de la fonction sur cet intervalle.
Définition
Un extremum est un minimum ou un maximum.
Extremum local
Soit $f$ une fonction définie sur l'ensemble $D_f$.
Soit $a$ un réel de $D_f$ et I un intervalle ouvert contenant $a$.
Si la restriction de $f$ à $D_f⋂I$ possède un extremum en $a$ , alors on dit que la fonction $f$ a un extremum local en $a$.
Cette définition compliquée n'est pas à savoir. Comprendre intuitivement ce qu'est un extremum local suffit.
Définition
L'intérieur d'un intervalle I est le plus grand intervalle ouvert inclus dans I.
Par exemple, l'intérieur de $[0;11[$ est $]0;11[$.
Propriété
Soit I un intervalle et $a$ un réel situé dans l'intérieur de I ($a$ n'est pas une borne de I).
Si $f$ est dérivable sur I et admet un extremum local en $a$, alors $f\,'(a)=0$,
et la tangente à $C_f$ en $a$ est alors parallèle à l'axe des abscisses.
Attention !
Si $f$ est dérivable sur I et admet un extremum local en $a$, et si $a$ est à l'extrémité de I, alors on ne connaît pas la valeur de $f\,'(a)$.
De plus, comme la réciproque de cette propriété est fausse, il est possible que $f\,'(a)=0$ sans que $f$ admette un extremum local en $a$.
 Exemple
Exemple
La fonction $f$, dérivable sur $]- ∞;10]$, admet le tableau de variation suivant.
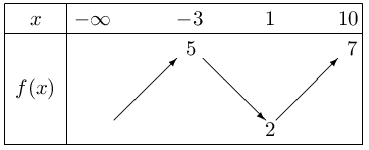
Déterminer, si possible, les valeurs de $f'(-3)$, $f'(1)$ et $f'(10)$.
Corrigé
La fonction $f$ est dérivable sur $]- ∞;10]$.
Or, d'après le tableau de variation, $-3$ est à l'intérieur de $]- ∞;10]$, et $f$ y admet un maximum local.
Par conséquent: $f'(-3)=0$.
De même, $1$ est dans l'intérieur de $]- ∞;10]$, et $f$ y admet un minimum local.
Par conséquent: $f'(1)=0$.
Par contre, 10 n'est pas dans l'intérieur de $]- ∞;10]$ (c'est une borne de l'intervalle).
Donc, bien que $f$ y admette un maximum local (c'est même le maximum absolu de la fonction), on ne peut rien conclure quant à la valeur de $f'(10)$.
 Exemple
Exemple
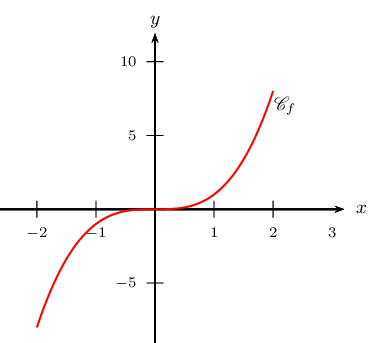
On considère la fonction cube $f$, définie par $f(x)=x^3$ pour tout $x$ de $\ℝ$.
Calculer $f'(0)$.
Peut-on en déduire que $f(0)$ est un extremum local de $f$?
Corrigé
On a: $f'(x)=3x^2$.
Donc $f'(0)=3×0^2=0$.
Donc la tangente à $C_f$ en $0$ est parallèle à l'axe des abscisses.
Mais on ne peut pas en déduire que $f(0)$ est un extremum local de $f$ car la réciproque de la propriété ci-desus est fausse.
En fait, comme chacun sait, $f(0)$ n'est pas un extremum local.