Fonction valeur absolue
Exercice 4
Soit $f(x)=$|$2x-3$|
Ecrire $f(x)$ sans utiliser de valeur absolue en vous plaçant sur des intervalles convenables.
Déterminer $f'x)$ en vous plaçant sur des intervalles convenables.
En revenant à la définition, montrer que $f'(1,5)$ n'existe pas.
Tracer rapidement l'allure de la courbe représentative de $f$.-
Soit $g(x)=√{(2x-3)^2}$
$g'(1,5)$ existe-t-il?
Corrigé
- On va utiliser la propriété: si $z$ est positif, alors |$z$|$=z$ , et si $z$ est négatif, alors |$z$|$=-z$.
On cherche le signe de $2x-3$.
C'est une fonction affine, qui s'annule pour $x=1,5$. Comme son coefficient directeur $2$ est strictement positif, elle est strictement négative pour $x<1,5$, et strictement positive pour $x>1,5$.
Donc: sur $]-\∞;1,5]$, on a: $f(x)=-(2x-3)=-2x+3$.
Sur $[1,5;+\∞[$, on a: $f(x)=2x-3$.
Sur $]-\∞;1,5[$, on obtient donc: $f'(x)=-2$
Sur $]1,5;+\∞[$,on obtient donc: $f'(x)=2$
On rappelle que, s'il existe, alors $f'(1,5)= \lim↙{h→0}r(h)$, où $r(h)={f(1,5+h)-f(1,5)}/{h}$ pour $h$ non nul.
Or, pour $h$<$0$, on a: $r(h)={-2(1,5+h)+3-0}/{h}={-3-2h+3}/{h}={-2h}/{h}=-2$.
Et par là: $\lim↙{h→0^-}r(h)=-2$.
De même, pour $h$>$0$, on a: $r(h)={2(1,5+h)-3-0}/{h}={3+2h-3}/{h}={2h}/{h}=2$.
Et par là: $\lim↙{h→0^+}r(h)=2$.
Et comme une limite est unique, on en déduit que $\lim↙{h→0}r(h)$ n'existe pas, et par là, $f'(1,5)$ n'existe pas.
L'allure de $\C_f$ est donnée ci-dessous. On constate que la tangente en 1,5 n'existe pas, et par là, $f'(1,5)$ n'existe pas.
-
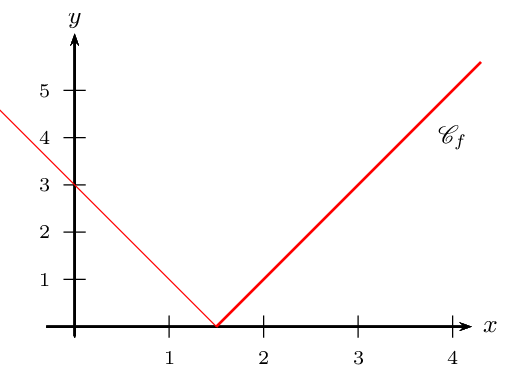
On a: $g(x)=√{(2x-3)^2}=$|$2x-3$|$=f(x)$.
Donc, d'après ce qui précède, $g'(1,5)$ n'existe pas.