 Algorithmes
Algorithmes
Exercice 1
Dans cet exercice, toute trace de recherche, même non aboutie, serait prise en compte lors de la notation
On considère un programme associé à l'algorithme suivant:
Lire $N$
$U$ ← 1000
$I$ ← 0
Tant que $I$<$N$
$U$ ← $0,95×U$
$I$ ← $I+1$
Fin du Tant que
Afficher $U$
1.a. Donner les valeurs successives prises par $I$ et $U$ lorsque le programme fonctionne pour une valeur de $N$ égale à 2.
Que s'affiche-t-il à la fin?
1.b. Compléter la ligne 5 du programme suivant (écrit en Python) pour qu'il soit conforme à l'algorithme proposé.
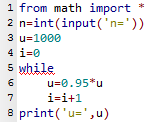
Quelques explications.
Les instructions d'entrée et de sortie ne sont pas exigibles dans un devoir, mais il est utile de les connaître.
La ligne 2 utilise la fonction input(). Cette fonction provoquera une interruption dans le programme et affichera une fenêtre contenant ici le texte 'n='.
Les caractères entrés par l'utilisateur seront alors transformés en entiers par la fonction int(),
puis ils seront affectés à la variable n.
La ligne 8 utilise la fonction print(). Cette fonction affichera dans la console le texte 'u=', suivi de la valeur de la variable u.
2. Soit $(u_n)$ la suite définie par:
la relation de récurrence $u_{n+1}=0,95×u_n$
son premier terme $u_0=1000$.
Préciser l'utilité de ce programme relativement à la suite proposée.
3.a. Supprimer une ligne de l'algorithme précédent, puis en modifier deux lignes pour que le nouvel algorithme permette de déterminer le plus petit
entier naturel $n$ tel que $u_n<900$.
3.b. Ecrire en Python un programme correspondant à l'algorithme modifié.
4.a. Ecrire un algorithme donnant le même résultat que celui donné au début de l'énoncé, mais en remplaçant la boucle Tant que par une boucle Pour.
4.b. Ecrire en Python un programme correspondant à l'algorithme modifié.
Corrigé
1.a. $N=2$; $U=1000$; $I=0$.
Première boucle (on a bien $I<2$):
$U=0,95×1000=950$ ; $I=1$.
Fin de la première boucle.
Seconde boucle: (on a bien $I<2$):
$U=0,95×950=902,5$ ; $I=2$.
Fin de la seconde boucle.
Il n'y a pas de troisième boucle car $I≥2$.
Finalement, il s'affiche la valeur de $U$, c'est à dire 902,5.
1.b. Voici le programme correct.
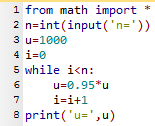
Noter le : en bout de la ligne 5.
Remarquer que le contenu de la boucle while est indenté (c'est à dire décalé vers la droite).
2.
Le programme proposé demande à l'utilisateur de saisir une valeur de $n$ et affiche alors la valeur de $u_n$ correspondante.
Par exemple, pour $n=2$, le programme renvoie la valeur de $u_2$, c'est à dire 902,5.
3.a. Nouvel algorithme:
(Noter que la ligne Lire $N$ a disparu)
$U$ ← 1000
$I$ ← 0
Tant que $U≥900$ (Noter le $U≥900$ à la place de $I$<$N$)
$U$ ← $0,95×U$
$I$ ← $I+1$
Fin du Tant que
Afficher $I$ (Noter le $I$ à la place de $U$)
Remarque: si l'on fait fonctionner cet algorithme, il s'affichera finalement 3 (car $u_3=857,375$ est la première valeur de $u_n$ en dessous de
900).
3.b. Voici un programme correct.
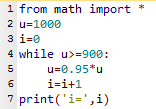
4.a. Algorithme équivalent à celui du début:
Lire $N$
$U$ ← 1000
Pour $I$ allant de 0 à $N-1$
$U$ ← $0,95×U$
Fin du Pour
Afficher $U$
(Noter qu'il est inutile d'augmenter $I$ de 1; l'incrémentation est automatique à la fin de chaque boucle Pour)
4.b. Voici un programme correct.

On rappelle que range(n) est une liste contenant les entiers de 0 à n-1.
La ligne 4 est alors l'instruction qui va donner à i toutes les valeurs de cette liste d'entiers, en passant d'une valeur à la suivante au début de chaque boucle.
i vaudra 0, puis 1, puis...etc...jusqu'à ce que i vaille n-1.