 Algorithmes
Algorithmes
Exercice 2
Dans cet exercice, toute trace de recherche, même non aboutie, serait prise en compte lors de la notation
On considère un programme associé à l'algorithme suivant:
fonction suite($N$)
$U$ ← 4
Pour $I$ allant de 0 à $ N-1$
$U$ ← $3×U$
Fin du Pour
Retourner $U$
1.a. Donner les valeurs successives prises par $I$ et $U$ lorsque le programme fonctionne pour une valeur de $N$ égale à 2.
1.b. Le programme ci-dessous, écrit en Python, devrait correspondre à l'algorithme précédent. Mais il comporte 2 lignes erronées. Corriger les 2 fautes.
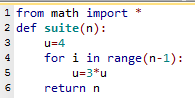
2. Définir une suite $(u_n)$ pour laquelle ce programme présente un intérêt.
Préciser l'utilité de ce programme relativement à la suite proposée.
3. Parmi les 3 algorithmes suivants, un seul est équivalent à l'algorithme initial
Lequel est-ce? (inutile de justifier)
Expliquer pourquoi les 2 autres algorithmes ne conviennent pas.
Algorithme 1
fonction suite($N$)
$U$ ← 4
$I$ ← 0
Tant que $I≤N$
$U$ ← $3×U$
$I$ ← $I+1$
Fin du Pour
Retourner $U$
Algorithme 2
fonction suite($N$)
$U$ ← 4
$I$ ← 0
Tant que $I$<$N$
$U$ ← $3×U$
$I$ ← $I+1$
Fin du Pour
Retourner $U$
Algorithme 3
fonction suite($N$)
$U$ ← 4
$I$ ← 0
Tant que $I$<$N$
$U$ ← $3×U$
Fin du Pour
Retourner $U$
4. Proposer l'algorithme d'une fonction qui ne contient pas de boucle, et qui permet d'obtenir la valeur de $u_n$ pour tout entier naturel $n$ saisi par l'utilisateur.
Solution...
Corrigé
1.a. on sait que: $N=2$;
$U=4$.
Juste avant la première boucle: $I=0$
Première boucle: (on a bien $I≤1$); $U=3×4=12$;
Fin de la première boucle; $I$ est augmenté automatiquement de 1, et vaut donc 1.
Seconde boucle: (on a bien $I≤1$); $U=3×12=36$;
Fin de la seconde boucle; $I$ est augmenté automatiquement de 1, et vaut donc 2.
Il n'y a pas de troisième boucle car $I>1$.
Finalement, la fonction retourne la valeur de $U$, c'est à dire 36.
1.b. Les lignes 4 et 6 étaient fausses.
Voici le programme correct.

Dans la ligne 4, range(n) est une liste contenant les entiers de 0 à n-1.
La ligne 8 ne fait pas partie de la fonction suite(n). Elle permet, à l'exécution du programme, d'afficher la valeur de suite(2) dans la console.
Pour obtenir le même résultat sans cette ligne, il faut écrire suite(2) dans la console après avoir exécuté le programme.
2. Une suite convenable est la suite $(u_n)$ définie par:
la relation de récurrence $u_{n+1}=3×u_n$
et son premier terme $u_0=4$.
Notons ici que la suite $(u_n)$ est géométrique de raison 3.
On obtient facilement $u_1=12$ et $u_2=36$.
Le programme proposé est une fonction de $n$ qui renvoie la valeur de $u_n$ correspondante.
Par exemple, pour $n=2$, le programme renvoie la valeur de $u_2$, c'est à dire 36.
3. L'algorithme correct est le second.
Le premier algorithme ne convient pas, car, par exemple, pour $N=0$, il devrait retourner 4, mais il retournera 12 (car la première boucle va s'effectuer).
Le troisième algorithme ne convient pas, car, par exemple, pour $N=1$, les boucles vont s'enchaîner sans jamais s'arrêter, car $I$ reste constamment à 0, et par là,
la condition $I$<$N$ est toujours vérifiée!
4. On a vu au 2. que la suite $(u_n)$ est géométrique de raison 3 et de premier terme $u_0=4$.
On obtient donc la formule explicite: $u_n=4×3^n$, valide pour tout entier naturel $n$.
D'où l'algorithme suivant:
fonction suite($N$)
$U$ ← $4×3^N$
Retourner $U$