 Algorithmes
Algorithmes
Exercice 5
Dans cet exercice, toute trace de recherche, même non aboutie, serait prise en compte lors de la notation
On considère un programme associé à l'algorithme ci-dessous.
Lire $A$
Lire $B$
Lire $L$
Lire $N$
Pour $I$ allant de 1 à $N$
$M$ ← ${A+B}/{2}$
Si $f(M)>L$
Alors $B$ ← $M$
Sinon $A$ ← $M$
Fin du Si
Fin du Pour
Afficher $A$ et $B$
La fonction $f$ citée dans l'algorithme est connue du programme.
Elle est supposée strictement croissante.
La valeur de $L$ saisie est supposée comprise entre $f(A)$ et $f(B)$.
1.a. On suppose que $f(x)=x^3+x$.
On suppose que les valeurs saisies pour $A$, $B$, $L$ et $N$ sont respectivement égales à: 0, 2, 5 et 3.
Ainsi, après les 4 premières lignes de l'algorithme, on obtient $A=0$, $B=2$, $L=5$ et $N=3$.
Donner les valeurs successives prises par $A$, $B$, $I$, et $M$ lorsque le programme continue de fonctionner.
1.b. Compléter les lignes 9, 12, 13 et 14 pour que le programme ci-dessous, écrit en Python, corresponde à l'algorithme précédent.

2.a. A quoi sert le programme?
2.b. $f$ est supposée strictement croissante: quel est l'intérêt de cette hypothèse?
2.c. Que se passe-t-il si $L$ n'est pas comprise entre $f(A)$ et $f(B)$?
3. On veut écrire un algorithme ayant la même fonction que le précédent, mais tel que la distance entre les nombres $A$ et $B$ affichés à la fin du
programme soit inférieure ou égale à une valeur $D$ saisie par l'utilisateur.
Un seul des algorithmes ci-dessous convient.
Donner sans justifier l'algorithme convenable.
Qu'affiche-t-il pour $A=0$, $B=2$, $L=5$ et $D=0,6$ (inutile de détailler).
Expliquer pourquoi l'autre algorithme ne convient pas.
Lire $A$
Lire $B$
Lire $L$
Lire $D$
Tant que $B-A$<$D$
Si $f({A+B}/{2})>L$
Alors $B$ ← ${A+B}/{2}$
Sinon $A$ ← ${A+B}/{2}$
Fin du Si
Fin du Tant que
Afficher $A$ et $B$
Lire $A$
Lire $B$
Lire $L$
Lire $D$
Tant que $B-A$>$D$
Si $f({A+B}/{2})>L$
Alors $B$ ← ${A+B}/{2}$
Sinon $A$ ← ${A+B}/{2}$
Fin du Si
Fin du Tant que
Afficher $A$ et $B$
Corrigé
1.a. Les 4 premières lignes de l'algorithme nous donnent: $A=0$, $B=2$, $L=5$ et $N=3$.
Juste avant la première boucle: $I=1$
Première boucle: (on a bien $I≤3$); $M={0+2}/{2}=1$;
On calcule $f(M)=2$. On n'a pas $f(M)>L$.
Par conséquent, on obtient: $A=1$.
Fin de la première boucle: $I$ est augmenté automatiquement de 1, et vaut donc 2.
Seconde boucle: (on a bien $I≤3$); $M={1+2}/{2}=1,5$;
On calcule $f(M)=4,875$. On n'a pas $f(M)>L$.
Par conséquent, on obtient: $A=1,5$.
Fin de la seconde boucle: $I$ est augmenté automatiquement de 1, et vaut donc 3.
Troisième boucle: (on a bien $I≤3$); $M={1,5+2}/{2}=1,75$;
On calcule $f(M)=7,1093$. On a $f(M)>L$.
Par conséquent, on obtient: $B=1,75$.
Fin de la troisième boucle: cette boucle est la dernière car $I$ valait 3 au début de la boucle.
Il n'y a pas de quatrième boucle.
Finalement, il s'affiche la dernière valeur de $A$, c'est à dire 1,5 et la dernière valeur de $B$, c'est à dire 1,75.
1.b. Voici le programme correct.
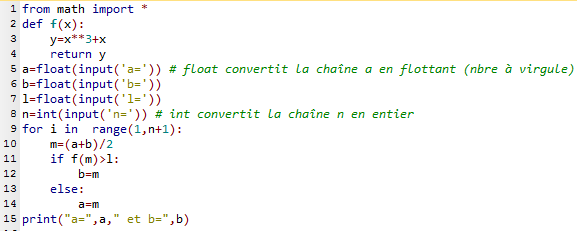
La ligne 9 aurait pu être: for i in range(n):
L'entier i prendrait alors les valeurs de 0 à n-1.
Ce n'est pas gênant car, comme dans le programme proposé, la boucle for serait parcourue n fois.
.
2.a. Le programme affiche deux nombres $A$ et $B$ qui encadrent la solution de l'équation $f(x)=L$.
2.b. La stricte croissance de $f$ assure l'unicité de la solution.
2.c. Si $L$ n'est pas comprise entre $f(A)$ et $f(B)$, alors l'équation n'a pas de solution entre $A$ et $B$. Les valeurs de $A$ et $B$ n'encadrent
rien!
Remarquons que, si la valeur de $L$ est comprise entre $f(A)$ et $f(B)$, et si $f$ est strictement croissante, alors l'équation $f(x)=L$ admet au plus une solution entre $A$ et $B$.
Mais il n'est pas certain que cette solution existe. Nous admettrons que la fonction $f$ proposée est suffisamment "sympathique" pour que la solution cherchée existe.
3. L'algorithme correct est le second.
Pour $A=0$, $B=2$, $L=5$ et $D=0,6$, il s'affiche finalement 1,5 (c'est $A$) et 1,75 (c'est $B$).
Le premier algorithme ne convient pas, car, par exemple, pour les valeurs précédentes, il affichera 0 et 2 (car la boucle ne va jamais s'effectuer).