Algorithmes
Exercice 7
Quelques informations pour commencer.
Considérons une expérience à 2 issues, appelées "succés" et "échec".
Supposons que la probabilité de "succès" vaille p (avec $p$ entre $0,2$ et $0,8$).
Si l'on répète $n$ fois de suite cette expérience (avec $n≥25$) et si les expériences sont indépendantes, alors la probabilité que la fréquence de "succès" soit dans l'intervalle
$I=[p-{1}/{√n};p+{1}/{√n}]$ vaut au moins $0,95$.
Cet intervalle $I$ s'appelle intervalle de fluctuation de $f$ au seuil de $95\%$.
Ici, l'expérience consiste à lancer un dé.
Appelons "succès" le fait d'obtenir un 5 ou un 6 sur un lancer de dé.
La probabilité de succès vaut $p={2}/{6}={1}/{3}≈0,33$
Supposons que l'on lance $n=100$ fois de suite ce dé.
On peut utiliser l'intervalle de fluctuation précédent car $n≥25$ et $p$ est entre $0,2$ et $0,8$.
Cet intervalle de fluctuation est alors: $I=[{1}/{3}-{1}/{√{100}};{1}/{3}+{1}/{√{100}}]≈[0,23:0,43]$
Par conséquent, si l'on lance $100$ fois de suite un dé, alors la probabilité que la fréquence de "succès" soit dans l'intervalle $[0,23;0,43]$ vaut au moins $0,95$.
On considère alors le programme en Python ci-dessous.
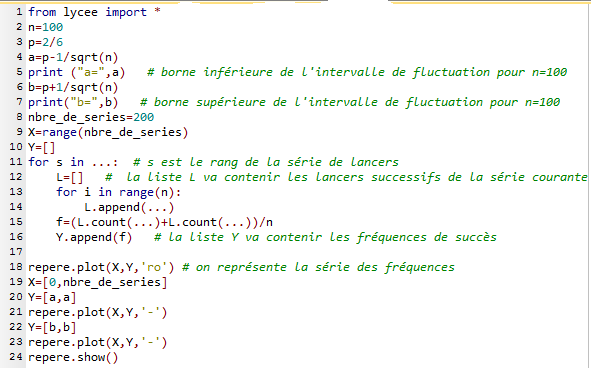
Ce programme simule 200 séries de 100 lancers de dé chacune.
Pour chaque série, le programme calcule la fréquence de "succès".
Le programme génère progressivement une liste des 200 fréquences de "succès".
Il s'agit de la liste Y de ce programme.
- Que valent les variables a et b de ce programme?
- Que contient la liste X?
- On rappelle que, si e et f sont des entiers naturels, alors l'instruction randint(e,f) renvoie un entier aléatoire compris entre e et f.
Compléter les lignes 11, 14 et 15 pour que le programme fonctionne. 
A quoi sert la ligne 18?- Que tracent les lignes 21 et 23?
- En quoi la figure obtenue permet-elle de confirmer expérimentalement la validité de la propriété:
si l'on lance $100$ fois de suite un dé, alors la probabilité que la fréquence de "succès" soit dans l'intervalle $[0,23;0,43]$ vaut au moins $0,95$.
Corrigé
Voici un programme complété correctement.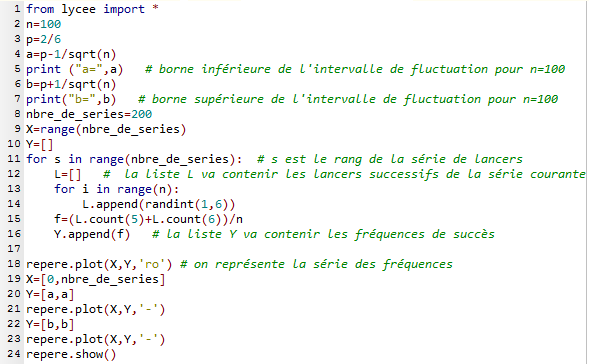
- Les variables a et b sont les bornes de l'intervalle de fluctuation de $f$ au seuil de $95\%$.
Comme $n=100$ et $p={1}/{3}$, ces bornes sont $a≈0,23$ et $b≈0,43$. - La liste X contient les entiers de 0 à nbre_de_series - 1, c'est à dire de 0 à 199.
- La ligne 11 permet de répéter les séries de n lancers de dé (c'est à dire 100 lancers de dé).
Le nombre de séries est nbre_de_series (c'est à dire 200).
Une ligne 11 correcte est donc:
for s in range(nbre_de_series):
Comme L'instruction randint(1,6) renvoie un entier aléatoire compris entre 1 et 6.
Une ligne 14 correcte est donc:
L.append(randint(1,6))
f est la fréquence de succès de la série courante.
Or un "succès" est le fait d'obtenir un 5 ou un 6 sur un lancer de dé.
Une ligne 15 correcte est donc:
f=(L.count(5)+L.count(6))/n - La ligne 18 permet de tracer un ensemble de points dont les abscisses successives sont dans la liste X, et dont les ordonnées successives sont dans la liste
Y.
Ainsi, le premier point aura pour abscisse 0, et pour ordonnée la fréquence de succès de la première série de 100 lancers de dé.
Et le second point aura pour abscisse 1, et pour ordonnée la fréquence de succès de la seconde série de 100 lancers de dé.
Et ainsi de suite jusqu'au 200ème point.
Le paramètre 'ro' permet de tracer les points en rouge. - Les lignes 21 et 23 tracent respectivement la droite horizontale d'équation y=a et la droite horizontale d'équation y=b
- Voici la figure produite par un lancement de ce programme.
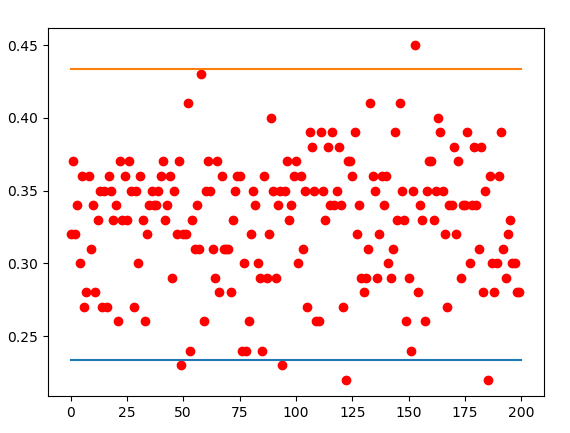
Si le programme est relancé, la figure obtenue sera certainement différente, car les fréquences de succès seront différentes. C'est ce qu'on appelle la fluctuation d'échantillonnage.
Mais il est fort probable que le nombre de points situés à l'extérieur de la bande délimitée par les 2 droites horizontales sera faible, plus précisément inférieur à $5\%$ de 200, c'est à dire plus petit que 10.
Cela valide expérimentalement la propriété proposée.