La Spécialité Maths en Première

Corrigé

Le plan est rapporté au repère orthonormé $(O,I,J)$.
Soient $A(-2;4)$, $B(2;-1)$ et $C(4;0)$ trois points.

1. On a: ${CB}↖{→}(x_B-x_C;y_B-y_C)=(2-4;-1-0)=(-2;-1)$
2. La droite (BC) admet ${CB}↖{→}$ comme vecteur directeur.
   Or ${CB}↖{→}(-2;-1)$
   On pose: $-b=-2$ et $a=-1$; soit: $b=2$ et $a=-1$
   Donc la droite (BC) admet une équation cartésienne du type: $-1x+2y+c=0$.
   Or cette droite passe par $C(4;0)$.
   Donc: $-1×4+2×0+c=0$.
   Et par là: $c=4$
   Donc une équation cartésienne de la droite (BC) est $-x+2y+4=0$
   A retenir: une droite de vecteur directeur ${u}↖{→}(-b; a )$ admet une équation cartésienne du type: $ax+by+c=0$.
   Pour information, elle admet aussi une équation cartésienne du type: $-ax-by+c=0$ (car $-{u}↖{→}(b; -a )$ en est aussi un vecteur directeur).
   


3. (BC) a pour équation cartésienne $-x+2y+4=0$
   Par conséquent, un vecteur normal à cette droite (BC) est, par exemple, le vecteur ${n}↖{→}(-1;2)$
   A retenir: une droite d'équation cartésienne $ax+by+c=0$ admet pour vecteur normal ${n}↖{→}(a; b )$.
   


4. Le point H est le projeté orthogonal de A sur (BC), donc le pied de la hauteur du triangle ABC issue de A.
   Donc (AH) est la hauteur de ABC issue de A.
   Et comme ${n}↖{→}(-1;2)$ est normal à (BC), la droite (AH) admet pour vecteur directeur ${n}↖{→}(-1;2)$.
   Donc cette droite (AH) admet une équation cartésienne du type: $-2x-1y+c=0$.
   Or cette droite passe par $A(-2;4)$.
   Donc: $-2×(-2)-1×4+c=0$.
   Et par là: $c=0$
   Donc une équation cartésienne de la droite (AH) est $-2x-y=0$
   


5. Les coordonnées du point H vérifient à la fois l'équation de (BC) et celle de (AH)
   Soit: $\{\table -x+2y+4=0\;\;\;(L_1); -2x-y=0\;\;\;(L_2)$
   Méthode 1: Nous allons procéder par combinaisons linéaires.
   $\{\table -x+2y+4=0\;\;\;(L_1); -2x-y=0\;\;\;(L_2)$ $⇔$ $\{\table -x+2y+4=0\;\;\; (L_1); -4x-2y=0\;\;\; (2L_2⇨L_2)$
             $⇔$ $\{\table -x+2y+4=0\;\;\; (L_1); -x+2y+4-4x-2y=0+0\;\;\; (L_1+L_2 ⇨L_2)$
            $⇔$ $\{\table -x+2y+4=0\;\;\; (L_1); -5x+4=0 \;\;\;(L_2)$
             $⇔$ $\{\table -x+2y+4=0; x={-4}/{-5}={4}/{5} $
             $⇔$ $\{\table -{4}/{5}+2y+4=0; x={4}/{5} $
             $⇔$ $\{\table 2y=-{16}/{5} ; x={4}/{5} $
             $⇔$ $\{\table y=-{8}/{5} ; x={4}/{5} $
   Donc la solution du système est le couple $(x;y)=(0,8\,$;$\,-1,6)$.
   
   Méthode 2: Nous allons procéder par substitutions.
   $\{\table -x+2y+4=0; -2x-y=0$ $⇔$ $\{\table -x+2y+4=0; y=-2x$
             $⇔$ $\{\table -x-4x+4=0; y=-2x$
             $⇔$ $\{\table x={-4}/{-5}={4}/{5}; y=-2×{4}/{5}=-{8}/{5}$
          Donc la solution du système est le couple $(x;y)=(0,8\,$;$\,-1,6)$.
   Finalement, H a pour coordonnées $(0,8\,$;$\,-1,6)$.
   La figure ci-dessous semble confirmer ce résultat.
   
   


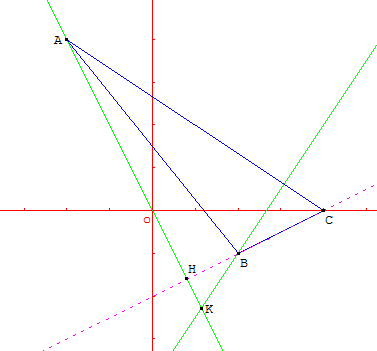
6. Pour montrer que la droite $d$ est la hauteur du triangle ABC issue de B, il suffit de montrer qu'elle passe par B et qu'elle est perpendiculaire à (AC).
   Or, comme son équation est $3x-2y-8=0$, elle admet pour vecteur normal ${u}↖{→}(3;-2)$
   Par ailleurs, on a: ${AC}↖{→}(x_C-x_A;y_C-y_A)=(4+2;0-4)=(6;-4)$
   Il est donc clair que ${AC}↖{→}=2{u}↖{→}$, et par là, ${AC}↖{→}$ est également un vecteur normal à $d$.
   La droite $d$ est donc bien perpendiculaire à (AC).
   Il reste à montrer qu'elle passe par B.
   C'est immédiat car on a: $3x_B-2yB-8=3×2-2×(-1)-8=0$.
   Finalement, la droite $d$ est bien la hauteur du triangle ABC issue de B
   


7. Le point K, orthocentre du triangle ABC, est à l'intersection de ses hauteurs, en particulier de (AH) et de $d$.
   Les coordonnées du point K vérifient à la fois l'équation de (AH) et celle de $d$
   Soit: $\{\table -2x-y=0\;\;\;(L_1); 3x-2y-8=0\;\;\;(L_2)$
   Nous allons procéder par combinaisons linéaires.
   $\{\table -2x-y=0\;\;\;(L_1); 3x-2y-8=0\;\;\;(L_2)$ $⇔$ $\{\table 4x+2y=0\;\;\; (-2L_1⇨L_1); 3x-2y-8=0\;\;\; (L_2)$
            $⇔$ $\{\table 4x+2y=0\;\;\; (L_1); 4x+2y+3x-2y-8=0+0 \;\;\;(L_1+L_2 ⇨L_2)$
             $⇔$ $\{\table 4x+2y=0; x={8}/{7} $
             $⇔$ $\{\table 4×{8}/{7}+2y=0; x={8}/{7} $
             $⇔$ $\{\table 2y=-{32}/{7} ; x={8}/{7} $
             $⇔$ $\{\table y=-{16}/{7} ; x={8}/{7} $
   Donc la solution du système est le couple $(x;y)=({8}/{7}\,$;$\,-{16}/{7})$.
   Le point K a donc pour coordonnées $({8}/{7}\,$;$\,-{16}/{7})$