 Géométrie repérée
Géométrie repérée
Exercice 2
Le plan est rapporté au repère orthonormé $(O,I,J)$.
Soient $A(-2;4)$ et $B(4;0)$ deux points.
- Quel est l'ensemble $\C_1$ des points dont les coordonnées vérifient l'équation $(x-1)^2+(y-2)^2=13$
- Déterminer une équation du cercle $\C_2$ de diamètre [AB].
- Que dire de $\C_1$ et $\C_2$?
- Déterminer les coordonnées du milieu K de [AB]
- Soit $M(0,8\,$;$\,-1,6)$. Montrer que M est sur $\C_1$.
- Que dire du triangle ABM?
- Déterminer les coordonnées des points U et V appartenant à l'intersection de $\C_1$ et de la droite $d$ d'équation $y=3$
Corrigé
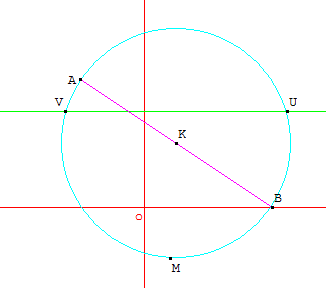
Le plan est rapporté au repère orthonormé $(O,I,J)$.
Soient $A(-2;4)$ et $B(4;0)$ deux points.
- L'ensemble $\C_1$ des points dont les coordonnées vérifient l'équation $(x-1)^2+(y-2)^2=13$ est le cercle de centre $E(1;2)$ et de rayon $√{13}$.
- $M(x;y)$ est sur $\C_2$ $⇔$ ${AM}↖{→}.{BM}↖{→}=0 $
Or ${AM}↖{→}(x+2;y-4)$ et ${BM}↖{→}(x-4;y)$
Donc: $M(x;y)$ est sur $\C_2$ $⇔$ $(x+2)×(x-4)+(y-4)×y=0$
Appelons (2) l'équation $(x+2)×(x-4)+(y-4)×y=0$
(2) est une équation du cercle $\C_2$. - Reprenons l'équation du cercle $\C_2$.
(2) $⇔$ $x^2-4x+2x-8+y^2-4y=0$
(2) $⇔$ $x^2-2x+y^2-4y=8$
Nous cherchons à faire apparaître les coordonnées du centre par la méthode de complétion du carré.
(2) $⇔$ $x^2-2×x×1+1^2-1^2+y^2-2×y×2+2^2-2^2=8$
(2) $⇔$ $(x-1)^2-1+(y-2)^2-4=8$
(2) $⇔$ $(x-1)^2+(y-2)^2=13$
On reconnaît l'équation du cercle $\C_1$.
Par conséquent, $\C_1$ et $\C_2$ sont confondus. - Les coordonnées du milieu K de [AB] sont:
${x_A+x_B}/{2}={-2+4}/{2}=1$ et ${y_A+y_B}/{2}={4+0}/{2}=2$
Donc on a: $K(1;2)$
Autre méthode:
Comme $\C_2$, cercle de diamètre [AB], est confondu avec $\C_1$, cercle de centre $E(1;2)$ et de rayon $√{13}$, on en déduit que le milieu K de [AB] est confondu avec E.
Donc on a: $K(1;2)$ - Soit $M(0,8\,$;$\,-1,6)$.
$\C_1$ a pour équation: $(x-1)^2+(y-2)^2=13$
Or, on a: $(x_M-1)^2+(y_M-2)^2=(0,8-1)^2+(-1,6-2)^2=13$
Donc le point M est sur $\C_1$. - Comme le point M est sur $\C_1$, cercle de diamètre [AB], et que ce point est distinct de A et de B, le triangle ABM est rectangle en M.
- Les coordonnées des points appartenant à l'intersection de $\C_1$ et de la droite $d$ d'équation $y=3$ sont telles que:
$(x-1)^2+(y-2)^2=13$ et $y=3$
Soit: $(x-1)^2+(3-2)^2=13$ et $y=3$
Soit: $(x-1)^2=12$ et $y=3$
Soit: ($x-1=√{12}$ ou $x-1=-√{12}$) et $y=3$
Soit: ($x=1+√{12}≈4,5$ et $y=3$) ou ($x=1-√{12}≈-2,5$ et $y=3$)
On obtient ainsi deux points
$U(1+√{12};3)$ et $V(1-√{12};3)$