 Géométrie repérée
Géométrie repérée
Exercice 3
Le plan est rapporté au repère orthonormé $(O,I,J)$.
Soient $\P$ la courbe d'équation $y=f(x)$, avec $f(x)=0,5(x^2-2x-3)$.
- Quelle est la nature de $\P$?
- Ecrire $f(x)$ sous forme canonique.
- Ecrire $f(x)$ sous forme factorisée.
- Soit $d_1$ la droite d'équation $x=2$.
Déteminer les coordonnées du (ou des) point(s) où $d_1$ coupe $\P$. - Soit $d_2$ la droite d'équation $y=3$.
Déteminer les coordonnées du (ou des) point(s) où $d_2$ coupe $\P$.
Corrigé
Le plan est rapporté au repère orthonormé $(O,I,J)$.
- On a: $f(x)=0,5(x^2-2x-3)= 0,5x^2-x-1,5$.
$f$ est donc un trinôme du second degré.
Par conséquent, $\P$ est une parabole. - Nous cherchons la forme canonique par la méthode de complétion au carré.
On a: $x^2-2x-3=x^2-2x+1^2-1^2-3$
Soit: $x^2-2x-3=(x-1)^2-1-3$
Soit: $x^2-2x-3=(x-1)^2-4$
Donc $f(x)=0,5((x-1)^2-4)$
Soit: $f(x)=0,5(x-1)^2-2$
On a bien écrit $f$ sous forme canonique. - $f$ est un trinôme avec $a=0,5$, $b=-1$ et $c=-1,5$.
$Δ=b^2-4ac=(-1)^2-4×0,5×(-1,5)=4$.
$Δ>0$. Le trinôme a 2 racines $x_1={-b-√Δ}/{2a}={1-2}/{1}=-1$ et $x_2={-b+√Δ}/{2a}={1+2}/{1}=3$.
Donc l'écritue de $f$ sous forme factorisée est:
$f(x)=0,5(x+1)(x-3)$ - Soit $d_1$ la droite d'équation $x=2$.
Soit $M(x;y)$ un point de $d_1$ et $\P$.
On a: $x=2$ et $y=f(x)$
Soit: $x=2$ et $y=f(2)=-1,5$
Il n'y a qu'un seul point convenable. Nommons le A.
On a: $A(2;-1,5)$.
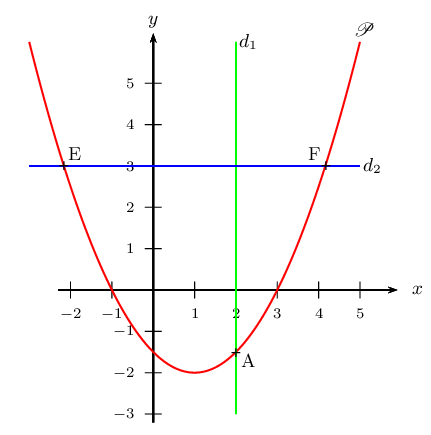
- Soit $d_2$ la droite d'équation $y=3$.
Soit $M(x;y)$ un point de $d_2$ et $\P$.
On a: $y=3$ et $y=f(x)$
Soit: $y=3$ et $3=0,5(x-1)^2-2$
Soit: $y=3$ et ${3+2}/{0,5}=(x-1)^2$
Soit: $y=3$ et ($√{10}=x-1$ ou $-√{10}=x-1$)
Soit: ($y=3$ et $√{10}+1=x$) ou ($y=3$ et $-√{10}+1=x$)
Il y a deux points convenables. Nommons les E et F.
On a par exemple: $E(1-√{10};3)$ et $F(1+√{10};3)$.