Géométrie repérée
Exercice 5
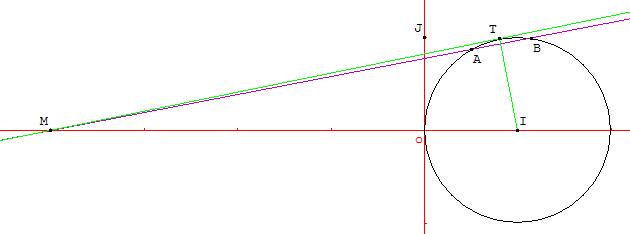
Il est conseillé de faire une figure, que l'on complètera au fur et à mesure.
Le plan est rapporté au repère orthonormé $(O,I,J)$.
Soit $C$ le cercle de centre I et de rayon 1.
Soit $M(-4;0)$.
- Montrer que $C$ admet pour équation cartésienne: $x^2-2x+y^2=0$
- Soit $A(0,5;y_A)$ avec $y_A>0$.
Montrer que le point $A$ appartient au cercle $C$ si et seulement si $y_A=0,5√{3}$. -
a. Déterminer une équation cartésienne de $(MA)$, puis son équation réduite.
b.
La droite $(MA)$ coupe le cercle $C$ en A et un un point B. Déterminer
les coordonnées de B.
c. Calculer alors le produit scalaire $ {MA}↖{→} .{MB}↖{→}$. - Soit $T(x_T;y_T)$ avec $y_T>0$.
On suppose que la droite $(MT)$ est tangente au cercle $C$ au point $T$.
a. Déterminer les coordonnées du point $T$.
b. Calculer alors le produit scalaire $ {MT}↖{→} .{MT}↖{→}$. - Soit $D(2;0)$. Vérifier que $ {MA}↖{→} .{MB}↖{→}={MT}↖{→} .{MT}↖{→}={MO↖{→} .{MD}↖{→}=MI^2-1^1$
Corrigé
- $N(x;y)∈C$ si et seulement si $IN^2=1^2$
$N(x;y)∈C$ si et seulement si $(x-1)^2+(y-0)^2=1$
$N(x;y)∈C$ si et seulement si $x^2-2x+1+y^2=1$
$N(x;y)∈C$ si et seulement si $x^2-2x+y^2=0$
Donc le cercle $C$ admet pour équation cartésienne: $x^2-2x+y^2=0$ - $C$ passe par le point $A(0,5;y_A)$ si et seulement si $0,5^2-2×0,5+y_A^2=0$
Soit: $0,25-1+y_A^2=0$
Soit: $y_A^2=0,75$
Soit: $y_A=√{0,75}$ ou $y_A=-√{0,75}$
Mais, comme $y_A>0$, on obtient: $y_A=√{0,75}=0,5√{3}$
Donc $C$ passe par le point $A$ si et seulement si $y_A=0,5√{3}$. -
a. On obtient facilement: $ {MA}↖{→}(4,5;0,5√3)$.
Donc la droite $(MA)$ admet une équation du type: $-0,5√3x+4,5y+c=0$.
Et comme cette droite passe par $M(-4;0)$, on a: $-0,5√3×(-4)+4,5×0+c=0$.
Et donc: $c=-2√3$.
Donc la droite $(MA)$ a pour équation cartésienne: $-0,5√3x+4,5y-2√3=0$.
En isolant $y$, on obtient l'équation réduite: $y={0,5√3x+2√3}/{4,5}$
Soit: $y={1}/{9}√3x+{4}/{9}√3$.
b. Un point de coordonnées $(x;y)$ est sur $(AM)$ et sur $C$ si et seulement si ses coordonnées vérifie l'équation réduite de $(AM)$ et une équation de $C$.
On a donc: $y={1}/{9}√3x+{4}/{9}√3$ et $x^2-2x+y^2=0$.
Par substitution dans l'équation de droite, on obtient: $x^2-2x+({1}/{9}√3x+{4}/{9}√3)^2=0$
Soit: $x^2-2x+({√3}/{9}(x+4))^2=0$
Soit: $x^2-2x+{3}/{81}(x^2+8x+16)=0$
Soit: $27x^2-54x+x^2+8x+16=0$ (en multipliant chaque membre par $27$)
Soit: $28x^2-46x+16=0$
Soit: $14x^2-23x+8=0$ (en multipliant chaque membre par $0,5$)
On obtient là un trinôme avec $a=14$, $b=-23$ et $c=8$.
$Δ=b^2-4ac=(-23)^2-4×14×8=281$.
$Δ>0$. Le trinôme a 2 racines $x_1={-b-√Δ}/{2a}={23-9}/{28}=0,5$ et $x_2={-b+√Δ}/{2a}={23+9}/{28}={8}/{7}$.
En remplaçant $x$ par sa valeur dans l'équation de $d_k$, on obtient:
pour $x=0,5$: $y=0,5√3$, et pour $x={8}/{7}$: $y={4}/{7}√3$.
On retrouve évidemment le point $A(0,5;0,5√3)$.
On obtient par ailleurs le point $B({8}/{7};{4}/{7}√3)$.
c. On obtient facilement: $ {MA}↖{→}(4,5;0,5√3)$ et ${MB}↖{→}({36}/{7};{4}/{7}√3)$.
D'où: $ {MA}↖{→} .{MB}↖{→}=4,5×{36}/{7}+0,5√3×{4}/{7}√3={162}/{7}+{6}/{21}={168}/{7}$
Soit: $ {MA}↖{→} .{MB}↖{→}=24$. - a. On obtient facilement: $ {MT}↖{→}(x_T+4;y_T)$ et ${TI}↖{→}(1-x_T;-y_T)$.
Or, la droite $(MT)$ est tangente au cercle $C$ au point $T$.
Donc: $ {MT}↖{→} .{TI}↖{→}=0$ et $x_T^2-2x_T+y_T^2=0$
Soit: $(x_T+4)×(1-x_T)+y_T×(-y_T)=0$ et $x_T^2-2x_T+y_T^2=0$
Soit: $x_T-{x_T}^2+4-4x_T-{y_T}^2=0$ et $x_T^2-2x_T+y_T^2=0$
Soit: $-{x_T}^2-3x_T-{y_T}^2+4=0$ et $x_T^2-2x_T+y_T^2=0$
En sommant les équations membre à membre, on obtient:
$-5x_T+4=0$
Et par là: $x_T=0,8$.
En remplaçant $x_T$ par sa valeur dans la seconde équation, on obtient: ${y_T}^2=0,96$
Et, comme $y_T>0$, on obtient: $y_T=√{0,96}=0,4√{6}$
Donc: $T(0,8;0,4√{6})$.
b. On obtient facilement: $ {MT}↖{→}(4,8;0,4√{6})$
D'où: $ {MT}↖{→} .{MT}↖{→}=4,8^2+(0,4√{6})^2=23,04+0,96=24$. - Soit $D(2;0)$. On obtient facilement: ${MO↖{→}(4;0)$ et ${MD}↖{→}(6;0)$
On a alors: ${MO↖{→} .{MD}↖{→}=4×6+0×0=24$
Par ailleurs, on obtient facilement: $MI^2-1^2=25-1=24$.
Donc, d'après le 3.c. et le 4.b., il est clair que:
$ {MA}↖{→} .{MB}↖{→}={MT}↖{→} .{MT}↖{→}={MO↖{→} .{MD}↖{→}=MI^2-1^2$
Ce résultat est généralisable:
pour tout point M et tout cercle $C$ de centre I de rayon $r$,
si une droite passant par M coupe $C$ aux points A et B (éventuellement confondus),
alors $ {MA}↖{→} .{MB}↖{→}=MI^2-r^2$.
La démonstration de ce cas général utilise le projeté orthogonal H du point I sur la droite $(AB)$.
Les meilleurs d'entre vous peuvent la chercher!