Géométrie repérée
Exercice 6
Le plan est rapporté au repère orthonormé $(O,I,J)$.
Soient $α$, $β$ et $e$ trois réels fixés. Le nombre $e$ est supposé non nul.
Soit $d$ la droite d'équation $y=β-e$.
Soit $F$ le point de coordonnées $(α ; β+e)$.
Partie A
Dans cette partie, on se place dans le cas particulier où $α=3$, $β=2$ et $e=2$
- Que dire de la droite $d$ dans ce cas?
- Quelles sont les coordonnées de F?
- Soit $M$ un point du plan. Soit $H$ le projeté orthogonal de $M$ sur la droite $d$.
On suppose que $FM=MH$.
Faire une figure sur laquelle on placera F et $d$ et le (ou les) point(s) $M$ convenable(s) dans chacun des cas suivants:
$FM=5$ $FM=4$ $FM=3$ $FM=2$ - Conjecturer la nature de la courbe $\sc P$ constituant l'ensemble des points M.
Soit $(x;y)$ les coordonnées d'un point $M$ de $\sc P$ dont le projeté orthogonal sur la
droite $d$ s'appelle $H$.
Quelles sont les coordonnées du point $H$?
Donner les coordonnées des vecteurs ${FM}↖{→}$ et ${MH}↖{→}$
Montrer que $FM=MH$ si et seulement si $y=f(x)$ avec $f(x)=0,125(x-3)^2+2$- De quelle nature est la fonction $f$?
Partie B
Dans cette partie, on se place dans le cas général où $α$, $β$ et $e$ sont trois réels fixés.
- Soit $(x;y)$ les coordonnées d'un point $M$ de $\sc P$ dont le projeté orthogonal sur la
droite $d$ s'appelle $H$.
Quelles sont les coordonnées du point $H$.
Vérifier que l'on a: ${FM}↖{→}(x-α;y-β-e)$ et ${MH}↖{→}(0;β-e-y)$
Montrer que $FM=MH$ si et seulement si $y=g(x)$ avec $g(x)={1}/{4e}(x-α)^2+β$.
Ce calcul est techniquement simple, mais il demande beaucoup de rigueur!
- De quelle nature est la fonction $g$?
Corrigé
Partie A
$α=3$, $β=2$ et $e=2$
- La droite $d$ a pour équation: $y=β-e$, soit: $y=2-2$, soit: $y=0$.
La droite $d$ est donc l'axe des abscisses. - Le point F a pour coordonnées $(α ; β+e)=(3 ; 2+2)=(3 ; 4)$
- Voici la construction des deux points M tels que $FM=3$.
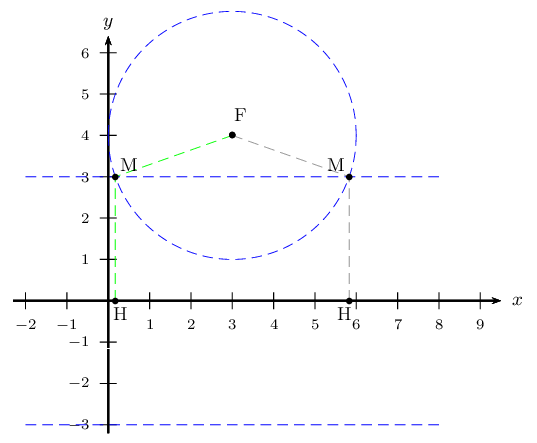
On a tracé un cercle de rayon 3 et de centre F.
Puis on a tracé les deux droites parallèles à $d$ (l'axe des abscisses) et situées à une distance de 3 de la droite $d$. Une seule coupe le cercle précédent.
Les deux points situés à l'intersection de la droite et du cercle conviennent.
On procède de même pour tous les autres points M.
On obtient à chaque fois deux points M, sauf pour $FM=2$ qui donne un seul point.
D'où la figure ci-dessous
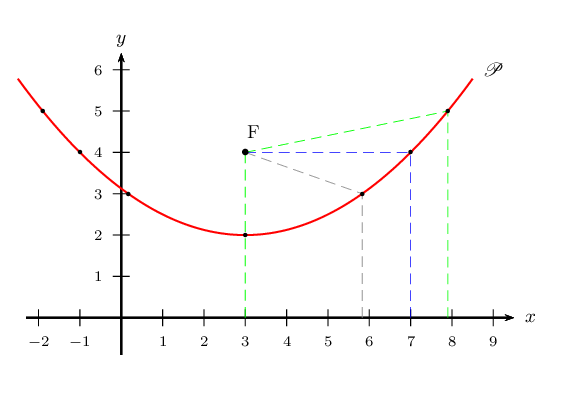
- Tous les points se trouvent sur la courbe $\sc P$ qui semble être une parabole.
- Soit $(x;y)$ les coordonnées d'un point $M$ dont le projeté orthogonal sur la
droite $d$ (l'axe des abscisses) s'appelle $H$.
Le point $H$ a évidemment pour coordonnées $(x;0)$.
On obtient facilement: ${FM}↖{→}(x-3;y-4)$ et ${MH}↖{→}(0;-y)$
On a: $FM=MH$ $ ⇔$ $FM^2=MH^2$ (car les distances FM et MH sont nécessairement positives)
Soit: $FM=MH$ $ ⇔$ ${∥}{FM}↖{→}{∥}^2={∥}{MH}↖{→}{∥}^2$
Soit: $FM=MH$ $ ⇔$ $(x-3)^2+(y-4)^2=0^2+(-y)^2$
Soit: $FM=MH$ $ ⇔$ $(x-3)^2+y^2-2×y×4+4^2=0+y^2$
Soit: $FM=MH$ $ ⇔$ $(x-3)^2+y^2-8y+16=y^2$
Soit: $FM=MH$ $ ⇔$ $(x-3)^2+16=8y$
Soit: $FM=MH$ $ ⇔$ ${1}/{8}(x-3)^2+{16}/{8}=y$
Soit: $FM=MH$ $ ⇔$ $0,125(x-3)^2+2=y$
Soit: $FM=MH$ $ ⇔$ $y=f(x)$ avec $f(x)=0,125(x-3)^2+2$ c.q.f.d. - La fonction $f$ est un trinôme du second degré présenté sous forme canonique.
Partie B
Dans cette partie, on se place dans le cas général où $α$, $β$ et $e$ sont trois réels fixés.
- Soit $(x;y)$ les coordonnées d'un point $M$ de $\sc P$ dont le projeté orthogonal
sur la droite $d$ s'appelle $H$.
Le point $H$ a évidemment pour coordonnées $(x;β-e)$.
Le point F a pour coordonnées $(α ; β+e)$
Effectivement, on obtient facilement:
${FM}↖{→}(x-α;y-(β+e))=(x-α;y-β-e)$
et ${MH}↖{→}(x-x;β-e-y)=(0;β-e-y)$
On procède alors comme dans la partie A.
$FM=MH$ $ ⇔$ ${∥}{FM}↖{→}{∥}^2={∥}{MH}↖{→}{∥}^2$
Soit: $FM=MH$ $ ⇔$ $(x-α)^2+(y-β-e)^2=0^2+(β-e-y)^2$
Soit: $FM=MH$ $ ⇔$ $(x-α)^2+(y-β)^2-2×(y-β)×e+e^2=0+(β-e)^2-2×(β-e)×y+y^2$
Soit: $FM=MH$ $ ⇔$ $(x-α)^2+y^2-2βy+β^2-2ye+2βe+e^2=β^2-2βe+e^2-2βy+2ey+y^2$
Soit: $FM=MH$ $ ⇔$ $(x-α)^2-2ye+2βe=-2βe+2ey$
Soit: $FM=MH$ $ ⇔$ $(x-α)^2+4βe=4ey$
Soit: $FM=MH$ $ ⇔$ ${1}/{4e}(x-α)^2+β=y$
Soit: $FM=MH$ $ ⇔$ $y=g(x)$ avec $g(x)={1}/{4e}(x-α)^2+β$ c.q.f.d. - La fonction $g$ est un trinôme du second degré présenté sous forme canonique.