 Dérivation
Dérivation
Exercice 1
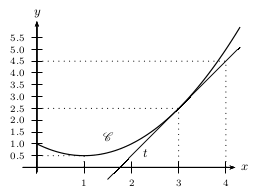
$f$ est représentée par $\C$.
$t$ est la tangente à $\C$ en 3.
Que vaut $f(1)$?
Que vaut $f\,'(1)$?
Que vaut $f(3)$?
Que vaut $f\,'(3)$?
Déterminer une équation de la tangente $t$.
Corrigé
$f(1)=0,5$.
$f\,'(1)$ est le coefficient directeur de la tangente à $\C$ en 1 (non tracée).
Cette tangente est parallèle à l'axe des absisses (car, entre autres, $f(1)$ est un minimum local).
Donc son coefficient directeur vaut 0.
Donc $f\,'(1)=0$.
$f(3)=2,5$.
$f\,'(3)$ est le coefficient directeur de la tangente $t$ à $\C_f$ en 3.
Or $t$ passe par les points de coordonnées (3;2,5) et (4;4,5).
Donc $t$ a pour coefficient directeur ${4,5-2,5}/{4-3}={2}/{1}=2$.
Donc $f\,'(3)=2$.
$t$ a une équation du type $y=2x+b$, car son coefficient directeur vaut 2.
$b$, ordonnée à l'origine, n'est pas lisible graphiquement. Trouvons le par le calcul.
Comme $t$ passe par le point $(3;2,5)$, les coordonnées de ce point vérifient l'équation de $t$.
Donc, on a: $2,5=2×3+b$. Soit: $2,5-6=b$. Soit: $-3,5=b$.
Donc $t$ a pour équation $y=2x-3,5$.
Autre méthode:
$t$ a pour équation: $y=f(3)+f\,'(3)(x-3)$.
Soit: $y=2,5+2(x-3)$.
Soit: $y=2,5+2x-6$.
Soit: $y=2x-3,5$.