 S'entraîner à l'épreuve anticipée
S'entraîner à l'épreuve anticipée
Exercice 1
Cet exercice permet d'évaluer la maîtrise des automatismes mathématiques; il concerne tous les élèves de première. Il peut constituer la première partie de l'épreuve anticipée.
Ceci est un QCM.
L'utilisation de la calculatrice est interdit.
Aucune justification n’est demandée et une seule réponse est possible par question.
- Question 1
Le double de l’inverse de 5 est égal à :
a. ${5}/{2}$ b. ${2}/{5}$ c. ${1}/{10}$ d. $-10$ - Question 2
On considère la relation $y=a-{bc}/{d}$ .
Lorsque $a={1}/{2}$, $b={1}/{7}$, $c=7$, $d=2$, la valeur de $y$ est égale à :
a. $-1,5$ b. $1$ c. ${76}/{154}$ d. $0$ - Question 3
Le prix d’un article est multiplié par 0,9.
Cela signifie que le prix de cet article a connu :
a. une baisse de $10%$ b. une baisse de $90%$ c. une baisse de $0,1%$ d. une hausse de $9%$ - Question 4
Le prix (non nul) d’un article est noté $p_0$. Ce prix augmente de $50%$ puis baisse de $50%$.
A l’issue de ces deux variations, le nouveau prix est noté $p_1$. On peut affirmer que :
a. $p_0=p_1$ b. $p_0$>$ p_1$
c. $p_0$<$p_1$ d. le résultat de la comparaison entre $p_0$ et $p_1$ dépend de la valeur de $p_0$ - Question 5
On lance un dé truqué à 6 faces. La probabilité d’obtenir chacune des faces est donnée dans le tableau ci-dessous :

On peut affirmer que :
a. $x=0,1$ b. $x=0,2$ c. $x=0,3$ d. $x=0,4$ - Question 6
On considère $a$, $b$, $c$ des réels non nuls tels que ${2}/{a}+b={1}/{z}$ .
On peut affirmer que :
a. $z={a}/{2}+{1}/{b}$ b. $z=2+ab$ c. $z={a}/{2+ab}$ d. $z={a}/{2+b}$ - Question 7
On a représenté ci-après la parabole d’équation $y=x^2$.

On note ($P$) l’inéquation, sur $ℝ$, $x^2<3$.
L’inéquation ($P$) est équivalente à :
a. $x$<$ 9$ b. $-√3$<$ x $<$ √3$ c. $x$>$√3$ d. $x=-√3$ ou $x=√3$ - Question 8
On a représenté ci-après une droite $d$ dans un repère orthonormé.
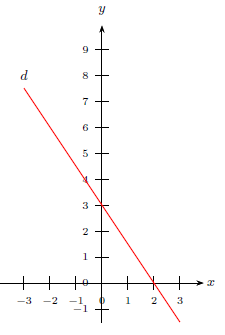
Une équation de la droite $d$ est :
a. $y=1,5x+3$ b. $y=-3x+2$ c. $3x+2y+6=0$ d. ${x}/{2}+{y}/{3}=1$ - Question 9
On considère trois fonctions définies pour tout $x$ de $ℝ$ par :
$f(x)=(x-1)^2+x^2$ $g(x)={1}/{3}+√3-x$ $h(x)={5x-{2}/{3}/{7}$
Parmi ces trois fonctions :
a. aucune n'est affine b. toutes sont affines
c. seule $g$ est affine d. $g$ et $h$ sont les deux seules fonctions affines - Question 10
On a représenté ci-après une courbe $P$.
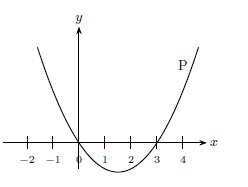
Une seule des quatre fonctions ci-dessous est susceptible d’être représentée par la courbe $P$. Laquelle ?
a. $x ↦ x^2+x$ b. $x ↦ x(x-3) $ c. $x ↦ -x(x-3) $ d. $x ↦ 3x$ - Question 11
On a représenté ci-après la courbe $C_f$ d’une fonction $f$.
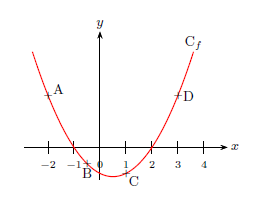
Les points A, B, C et D appartiennent à la courbe $C_f$.
Leurs abscisses sont notées respectivement $x_A$, $x_B$, $x_C$ et $x_D$.
L’inéquation $x×f(x)$>$0$ est vérifiée par :
a. $x_A$ b. $x_B$ c. $x_C$ d. $x_C$ et $x_D$ - Question 12
Voici une série de notes avec les coefficients associés.
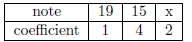
On note $m$ la moyenne de cette série. Que doit valoir $x$ pour que $m=15$ ?
a. 11 b. 13 c. 26 d. 10
Corrigé
Les explications ne sont pas exigées.
- Question 1
On calcule le double de l’inverse de 5 : $2×{1}/{5}={2}/{5}=0,4$
Réponse b. ${2}/{5}$ - Question 2
Lorsque $a={1}/{2}$, $b={1}/{7}$, $c=7$, $d=2$, la valeur de $y$ est égale à : ${1}/{2}-{{1}/{7}×7}/{2}={1}/{2}-{1}/{2}=0$
Réponse d. $0$ - Question 3
Le prix d’un article est multiplié par 0,9.
Or $0,9=90%=100%-10%$
Cela signifie que le prix de cet article a connu une baisse de $10%$.
Réponse a. une baisse de $10%$
- Question 4
Le prix (non nul) d’un article est noté $p_0$. Ce prix augmente de $50%$ puis baisse de $50%$.
A l’issue de ces deux variations, le nouveau prix est noté $p_1=p_0×(1+50%)×(1-50%)=p_0×1,5×0,5=p_0×0,75$.
Comme $0,75$<$1$, et que $p_0>0$, on en déduit que $p_0$<$p_1$.
Réponse c. $p_0$<$p_1$
- Question 5
La somme des probabilités des événements élémentaires vaut 1.
Donc: $0,1+0,2+0,3+0,1+0,2+x=1$
Soit: $0,9+x=1$.
Soit: $x=1-0,9=0,1$
Réponse a. $x=0,1$
- Question 6
On a: ${2}/{a}+b={1}/{z}$ .
Soit: ${2}/{a}+{b}/{1}={1}/{z}$ .
Soit: ${2}/{a}+{ab}/{a}={1}/{z}$ .
Soit: ${2+ab}/{a}={1}/{z}$ .
Soit: ${a}/{2+ab}={z}/{1}$.
Soit: ${a}/{2+ab}=z$
Réponse c. $z={a}/{2+ab}$
- Question 7
On résout graphiquement:
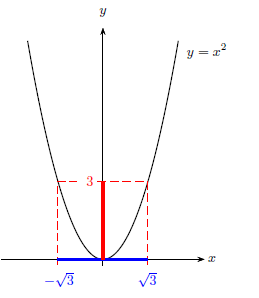
L’inéquation ($P$) est équivalente à $-√3$ < $ x $ < $ √3$
Réponse b. $-√3$ < $ x $ < $ √3$
- Question 8
Toutes les équations proposées sont bien des équations de droite (paramétriques ou cartésiennes). Cherchons laquelle convient.
Comme $d$ passe par $A(0,3)$ et $B(2,0)$, voyons si les coordonnées de ces 2 points vérifient les équations proposées.
On a: $1,5x_B+3=1,5×2+3=6$. Or $y_B=0$. Donc: $y_B≠1,5x_B+3$. Donc: B n'est pas sur la droite d'équation $y=1,5x+3$. Cette équation ne convient pas.
On a: $-3x_A+2=-3×0+2=2$. Or $y_A=3$. Donc: $y_A≠-3x_A+2$. Donc: A n'est pas sur la droite d'équation $y=-3x+2$. Cette équation ne convient pas.
On a: $3x_B+2y_B+6=3×2+2×0+6=12$. Donc: $3x_B+2y_B+6≠0$. Donc: B n'est pas sur la droite d'équation $3x+2y+6=0$. Cette équation ne convient pas.
Et comme une et une seule réponse est correcte c'est forcément la dernière.
Réponse d. ${x}/{2}+{y}/{3}=1$
Les inquiets peuvent contrôler que les coordonnées de A et de B vérifient bien cette équation.
- Question 9
On a: $f(x)=(x-1)^2+x^2=x^2-2x+1+x^2=2x^2-2x+1$ $f$ est un trinôme du second degré.
$g(x)={1}/{3}+√3-x=-x+{1}/{3}+√3$ $g$ est affine de coefficient directeur $-1$ et d'ordonnée à l'origine ${1}/{3}+√3$.
$h(x)={5x-2}/{3}/{7}={5x}/{{3}/{7}}-{2}/{{3}/{7}}=5x×{7}/{3}-2×{7}/{3}={35}/{3}x-{14}/{3}$ $h$ est affine de coefficient directeur ${35}/{3}$ et d'ordonnée à l'origine $-{14}/{3}$.
Réponse d. $g$ et $h$ sont les deux seules fonctions affines
- Question 10
La courbe $P$ représente une fonction parmi les 4 proposées.

L'image de 0 vaut 0. L'image de 3 vaut 0. L'image de 1 est strictement négative.
Voyons quelle fonction vérifie les 3 propositions.
Pour $x ↦ x^2+x$, on calcule : $3^2+3=9+3=12$. L'image de 3 ne vaut pas 0. Cette fonction ne convient pas.
Pour $x ↦ x(x-3)$, on calcule : $0×(0-3)=0 $ et $3×(3-3)=0$ et $1×(1-3)=-2 $. Donc l'image de 0 vaut 0, l'image de 3 vaut 0 et l'image de 1 est strictement négative. Il semble donc que cette fonction puisse convenir. Mais pour en être certain, il faut vérifier que les deux dernières fonction ne conviennent pas.
Pour $x ↦ -x(x-3)$, on calcule : $-1×(1-3)=2$. L'image de 1 n'est pas strictement négative. Cette fonction ne convient pas.
Pour $x ↦ 3x$, il est clair que cette fonction est linéaire et donc représentée par une droite. Elle ne peut donc pas convenir car $P$ n'est pas une droite !
Réponse b. $x ↦ x(x-3)$ - Question 11
On a représenté ci-après la courbe $C_f$ d’une fonction $f$.

L’inéquation $x×f(x)$>$0$ est vérifiée quand $x$ et $f(x)$ ont strictement le même signe.
Comme $x_A$<$0$ et $f(x_A)$>$0$, $x_A$ ne convient pas.
Comme $x_B$<$0$ et $f(x_B)$<$0$, $x_B$ convient.
Comme $x_C$>$0$ et $f(x_C)$<$0$, $x_C$ ne convient pas.
Comme $x_D$>$0$ et $f(x_D)$>$0$, $x_D$ convient.
Par conséquent, la seule proposition valide est la seconde.
Réponse b. $x_B$
- Question 12

On a: ${1×19+4×15+2×x}/{1+4+2}=m$
Soit: ${79+2x}/{7}=15$
Soit: $79+2x=7×15$
Soit: $2x=105-79$
Soit: $x={26}/{2}=13$
Réponse b. 13