 S'entraîner à l'épreuve anticipée
S'entraîner à l'épreuve anticipée
Exercice 2
Cet exercice permet d'évaluer la maîtrise des automatismes mathématiques; il concerne tous les élèves de première. Il peut constituer la première partie de l'épreuve anticipée.
Ceci est un QCM.
L'utilisation de la calculatrice est interdit.
Aucune justification n’est demandée et une seule réponse est possible par question.
- Question 1
On considère l’arbre de probabilité ci-après.
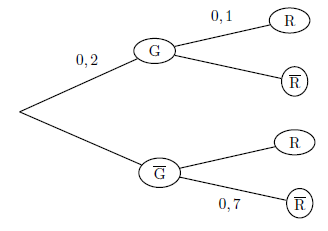
La probabilité de l’évènement $R$ est égale à :
a. $0,1$ b. $0,26$ c. $0,4$ d. $1$ - Question 2
Le prix d'un pull est de 300 euros. Il est baissé de $20%$. Après cette réduction, il vaut alors :
a. $280$ euros b. $240$ euros c. $207$ euros d. $60$ euros - Question 3
Une hausse de $40%$ suivi d'une baisse de $50%$ équivaut à :
a. une baisse de $10%$ b. une baisse de $20%$ c. une baisse de $30%$ d. une baisse de $70%$ - Question 4
Un magasin ne vend que des téléphones. Les appareils de moins de 300 euros représentent le tiers de ses ventes. Parmi eux, la moitié sont de marque SANSON.
Les téléphones de marque SANSON de moins de 300 euros vendus par ce magasin représentent :
a. un sixième des ventes b. cinq tiers des ventes
c. un cinquième des ventes d. cinq sixièmes des ventes - Question 5
Le nombre ${5^3×2}/{10^2}$ vaut :
a. $1$ b. $5^3$ c. ${5}/{2}$ d. $25$ - Question 6
La vitesse du son dans l'air à 15 °C au niveau de la mer est d'environ $1,224×10^3$ km/h.
Dans ces conditions, en une minute, le son parcourt environ :
a. $200$ mètres b. $300$ mètres c. $20,4$ km d. $240$ km - Question 7
Le plan est rapporté à un repère orthonormé. La droite passant par les points A(1;3) et B($-1$;$-2$) admet pour coefficient directeur :
a. $-2,5$ b. $0$ c. ${2}/{5}$ d. ${5}/{2}$ - Question 8
On a représenté ci-après une droite $d$ dans un repère orthogonal.
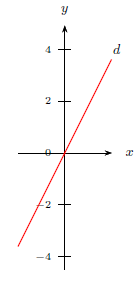
Une équation de la droite $d$ est :
a. $y=(x+1)^2-x^2-1$ b. $y=-3x$ c. $y=x+2$ d. $y=2x^2$ - Question 9
L'équation $x^2=3$ admet pour ensemble de solutions :
a. $∅$ b. $\{9\}$
c. $\{√3\}$ d. $\{-√3$;$√3\}$ - Question 10
La fonction $f$ définie sur $ℝ$ par $f(x)=(-x+2)(5x-3)$ admet pour tableau de signes :
a.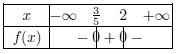 b.
b. 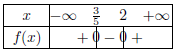
c.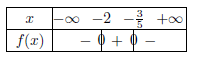 d.
d. 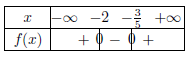
- Question 11
L'expression factorisée de $4x^2+0,25+2x$ est :
a. $(2x+0,5)^2$ b. $(x+0,5)^2$ c. $(x+1)^2$ d. $(2x+1)^2$ - Question 12
Chacun sait que l'aire $S$ d'un disque de rayon $r$ est donnée par l'égalité $S= πr^2$.
On peut en déduire que :
a. $r={S}/{π}$ b. $r=√{{S}/{π}}$ c. $√{{π}/{S}}$ d. $r=√{πS}$
Corrigé
Les explications ne sont pas exigées.
- Question 1
Voici l’arbre de probabilité complété.
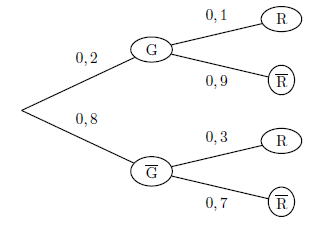
D'après la formule des probabilités totales, on a :
$p(R)=p(G∩R)+p(G↖{-}∩R)$ (par application de la formule des probabilités totales).
Soit: $p(R)=p(G)×p_G(R)+p(G↖{-})×p_{G↖{-}}(R)$ .
Soit: $p(R)=0,2×0,1+0,8×0,3=0,02+0,24=0,26$
Réponse b. $0,26$ - Question 2
Après la réduction de $20%$, le pull de 300 euros vaut :
$300×(100%-20%)=300×80%=300×0,80=240$ (euros).
Réponse b. $240$ euros - Question 3
Une hausse de $40%$ suivi d'une baisse de $50%$ est associée à un coefficient multiplicateur égal à :
$(100%+40%)×(100%-50%)=1,40×0,50=0,70=100%-30%$.
Et donc à une baisse de $30%$.
Réponse c. une baisse de $30%$ - Question 4
On calcule : ${1}/{3}×{1}/{2}={1}/{6}$
Les téléphones de marque SANSON de moins de 300 euros vendus par ce magasin représentent donc un sixième des ventes.
Réponse a. un sixième des ventes - Question 5
On a: ${5^3×2}/{10^2}={5^3×2}/{(5×2)^2}={5^3×2}/{5^2×2^2}={5}/{2}$
Réponse c. ${5}/{2}$ - Question 6
Une heure est composée de 60 minutes. Un kilomètre est composé de 1000 mètres.
On calcule donc: ${1,224×10^3×1000}/{60}≈{12×10^{-1}×10^3×10^3}/{6×10}≈2×10^{-1+3+3-1}≈2×10^4$.
Donc, en une minute, le son parcourt environ $20\, 000$ mètres, soit environ 20 kilomètres.
Réponse c. $20,4$ km - Question 7
Le plan est rapporté à un repère orthonormé. La droite passant par les points A(1;3) et B($-1$;$-2$) admet pour coefficient directeur :
${y_B-y_A}/{x_B-x_A}={-2-3}/{-1-1}={-5}/{-2}={5}/{2}$
Réponse d. ${5}/{2}$ - Question 8
On a représenté ci-après une droite $d$ dans un repère orthogonal.

La droite passe par l'origine est elle n'est pas parallèle à l'axe des ordonnées. Donc elle admet une équation du type $y=ax$.
Et comme elle représente une fonction linéaire strictement croissante, $a$ est strictement positif.
Par conséquent, les trois dernières propositions ne peuvent pas convenir.
Réponse a. $y=(x+1)^2-x^2-1$
Pour les inquiets, cette équation peut s'écrire : $y=x^2+2x+1$, soit $y=2x$, ce qui est conforme. - Question 9
L'équation $x^2=3$ admet pour ensemble de solutions $\{-√3$;$√3\}$.
Réponse d. $\{-√3$;$√3\}$ - Question 10
$f(x)=(-x+2)(5x-3)$ est un produit de deux fonctions affines.
On résout : $-x+2=0$ $ ⇔$ $2=x$
et $5x-3=0$ $ ⇔$ $x={3}/{5}=0,6$
Le coefficient directeur de $-x+2$ est $-1$ et il est strictement négatif.
Le coefficient directeur de $5x-3$ est $5$ et il est strictement positif.
D'où le tableau de signes.
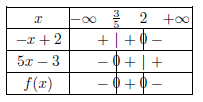
Réponse a.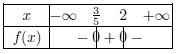
- Question 11
On factorise $4x^2+0,25+2x=(2x)^2+0,5^2+2×2x×0,5=(2x)^2+2×2x×0,5+0,5^2=(2x+0,5)^2$
Réponse a. $(2x+0,5)^2$ - Question 12
Chacun sait que l'aire $S$ d'un disque de rayon $r$ est donnée par l'égalité $S= πr^2$.
On peut en déduire que :
${S}/{π}=r^2$
Et, comme $r$ est positif: $r=√{{S}/{π}}$.
Réponse b. $r=√{{S}/{π}}$