S'entraîner à l'épreuve anticipée
S'entraîner à l'épreuve anticipée
Exercice 3
Ce sujet ne concerne que les élèves suivant la spécialité de mathématiques. Il peut constituer la seconde partie de l'épreuve anticipée.
L'utilisation de la calculatrice est interdit.
Partie 1
Une boîte contient 70 000 mouches; certaines sont atteintes par un virus X. La population globale est supposée rester constante.
Au début de l'expérience, la boîte contient 7 000 mouches malades, et 63 000 en pleine santé.
Chaque semaine, 20% des mouches malades guérissent; par contre, 20% des mouches saines deviennent malades.
Une mouche peut contracter plusieurs fois la maladie.
Soit $u_n$ le nombre de milliers de mouches malades après $n$ semaines. Il est clair que $u_0=7$.
1.a. Montrer que $u_1=18,2$
1.b. Montrer que $u_{n+1}=0,6×u_n+14$ pour tout naturel $n$.
2.a. On considère alors la suite $v_n$ définie par $v_n=u_n-35$, pour tout naturel $n$.
Montrer que la suite $(v_n)$ est géométrique de raison $a=0,6$.
2.b. Pour tout naturel $n$, exprimer $v_n$ en fonction de $n$.
2.c. Montrer que $u_n=(-28)×0,6^n+35$ pour tout naturel $n$.
3.a. Voici un extrait d’une feuille de tableur. Les valeurs des cellules de la ligne 2 sont arrondies à 0,001 près.
La ligne 2 a été complétée par recopie vers la droite d'une formule dans la cellule B2.

Les valeurs des cellules de la ligne 2 sont arrondies à 0,001 près.
Proposer une formule convenable.
3.b. Au bout de combien de semaines le nombre de mouches contaminées dépasse-t-il les 30 000 ?
Aide au calcul:
$7×0,80=5,6$ $63×0,20=12,6$ $70×0,20=14$ $0,6×35=21$
Partie 2
Le plan est rapporté à un un repère orthogonal.
1. On considère la fonction $g$ définie pour tout réel $x$ par $g(x)=x^2-x-6$.
On note $P$ la courbe représentative de la fonction $g$.
1.a. Étudier le signe de la fonction $g$ sur $ℝ$.
1.b. Étudier les variations de la fonction $g$ sur $ℝ$.
2. On considère la fonction $f$ définie pour tout réel $x$ de l’intervalle [-1 ; 3,3] par
$f(x)=x^3-x^2-6x$ .
On note $C$ la courbe représentative de la fonction $f$.
2.a. Vérifier que pour tout réel $x$ de l'intervalle [-1 ; 3,3] on a $f(x)=xg(x)$ .
2.b. A l’aide de la réponse à une question du 1., déterminer la position de la courbe $C$ par rapport à l’axe des abscisses.
2.c. On admet que la fonction $f$ est dérivable sur l’intervalle [-1 ; 3,3].
Déterminer $f'(x)$.
2.d. En déduire le tableau de variations de la fonction $f$ sur l’intervalle [-1 ; 3,3].
On admettra que $f(-1)=4$, $f({2+√{76}}/{6})≈-8,2$ et $f(3,3)≈5,2$
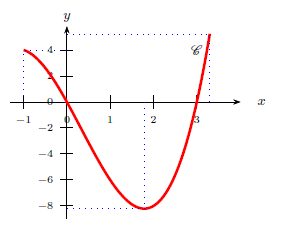
2.e. Réaliser un schéma de l’allure de la courbe $C$ sur lequel apparaîtront les résultats des questions 2.b et 2.d.
Aide au calcul:
$0,5^2-0,5-6=-6,25$ $4×3×6=72$ ${2-√{76}}/{6}≈-1,1$ ${2+√{76}}/{6}≈1,8$
Corrigé
Partie 1
1.a. $u_1=u_0×0,80+(70-u_0)×0,20=7×0,80+(70-7)×0,20=7×0,80+63×0,20=18,2$.
1.b. Pour tout naturel $n$: $u_{n+1}=u_n×0,80+(70-u_n)×0,20=0,80u_n+70×0,20-0,20u_n=0,6×u_n+14$.
2.a. Soit $n$ un entier naturel; on a: $v_n=u_n-35$, et $u_{n+1}=0,6×u_n+14$
Donc: $v_{n+1}=u_{n+1}-35=0,6×u_n+14-35=0,6×u_n-21$.
Or: $0,6×v_n=0,6×(u_n-35)=0,6×u_n-0,6×35=0,6×u_n-21$.
Donc: $v_{n+1}=0,6×v_n$, et ceci est vrai pour tout entier naturel $n$.
Donc $(v_n)$ est bien géométrique de raison $0,6$.
2.b. Notons que $v_0=u_0-35=7-35=-28$.
Comme $(v_n)$ est géométrique de raison $0,6$ et de premier terme $-28$,
on obtient: $v_n=(-28)×0,6^n$.
2.c. Par ailleurs, comme $v_n=u_n-35$, on obtient: $v_n+35=u_n$.
Ce qui donne finalement: $(-28)×0,6^n+35=u_n$.
3.a. Une formule convenable est : =(-28)*0,6^B1+35
3.b. Le nombre de mouches contaminées dépasse les 30 000 pour $n=4$, soit au bout de 4 semaines.
Partie 2
1.a. $g$ est un trinôme avec $a=1$, $b=-1$ et $c=-6$.
$Δ=b^2-4ac=(-1)^2-4×1×(-6)=25$.
$Δ>0$. Le trinôme a 2 racines $x_1={-b-√Δ}/{2a}={1-5}/{2}=-2$ et $x_2={-b+√Δ}/{2a}={1+5}/{2}=3$.
Et comme $a>0$, on obtient le tableau de signes suivant:
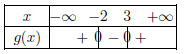
1.b. $g'x)=2x-1$.
$g'$ est affine, de coefficient $2>0$. On résout: $2x-1=0$ $⇔$ $x=0,5$.
Notons que $g(0,5)=0,5^2-0,5-6=-6,25$
D'où le tableau de variations de $g$ sur $ℝ$.
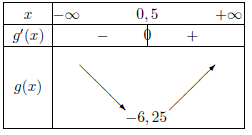
2.a. Pour tout réel $x$ de l'intervalle [-1 ; 3,3] on a: $xg(x)=x(x^2-x-6)=x^3-x^2-6x=f(x)$.
2.b. On s'intéresse uniquement aux réels de l'intervalle [-1 ; 3,3].
D'après le te tableau de signes de la question du 1.a., $g$ est strictement négative sur [-1 ; 3[, nulle en 3, et strictement positive sur ]3 ; 3,3].
Cela permet de dresser le tableau suivant.

Donc la courbe $C$ est strictement au dessus de l’axe des abscisses pour $x$ dans [-1 ;0[ ou dans ]3 ; 3,3]
et elle est strictement en dessous de l’axe des abscisses pour $x$ dans ]0 ; 3[.
Elle coupe l’axe des abscisses pour $x=0$ ou $x=3$.
2.c. Pour tout réel $x$ de l’intervalle [-1 ; 3,3] on a :
$f'(x)=3x^2-2x-6$.
2.d. $f'$ est un trinôme avec $a=3$, $b=-2$ et $c=-6$.
$Δ=b^2-4ac=(-2)^2-4×3×(-6)=76$.
$Δ>0$. Le trinôme a 2 racines $x_1={-b-√Δ}/{2a}={2-√{76}}/{6}≈-1,1$ et $x_2={-b+√Δ}/{2a}={2+√{76}}/{6}≈1,8$.
Et comme $a>0$, on obtient le tableau de suivant:

2.e. Voici un schéma de l’allure de la courbe $C$