S'entraîner à l'épreuve anticipée
S'entraîner à l'épreuve anticipée
Exercice 4
Ce sujet ne concerne que les élèves suivant la spécialité de mathématiques. Il peut constituer la seconde partie de l'épreuve anticipée.
L'utilisation de la calculatrice est interdit.
Partie 1
1. Déterminer le sens de variation de la fonction $g$ définie pour tout $x$ de $\ℝ$ par: $g(x)={1}/{3}x^3+{1}/{2}x^2-2x$.
2. En déduire le sens de variation de la suite $(u_n)$ définie pour $n≥1$ par $u_n=g(n)$
3. La suite $(t_n)$ définie pour $n≥0$ par $t_n=g(n)$ est-elle croissante?
Partie 2
Le plan est rapporté à un un repère orthonormé.
On considère les points
$A(2;-1)$ $B(0;3)$ $C(3;1)$.
1. Vérifier que ${AB}↖{→}.{AC}↖{→}=6$.
2. Calculer les distances $AB$ et $AC$, on donnera les valeurs exactes.
3. Déterminer la mesure de l'angle $A↖{∧}$ au degré près.
4. Vérifier qu'une équation cartésienne de la droite (AB) est: $2x + y − 3 = 0$.
5. On note H le pied la hauteur du triangle ABC issue du sommet C.
Déterminer les coordonnées du point H.
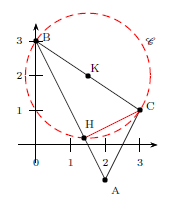
6.a. Soit $C$ le cercle de diamètre [BC].
Montrer que le cercle $C$ admet pour équation : $x^2-3x+y^2-4y+3=0$.
6.b. Le point H appartient-il au cercle $C$?
Aide au calcul:
$\cos52^°≈0,62$ $\cos53^°≈0,60$ $\cos54^°≈0,59$
$1,5^2=2,25$ $1,4^2=1,96$ $3×1,4=4,2$ $0,2^2-0,04$
Corrigé
Partie 1
1. On a: $g(x)={1}/{3}x^3+{1}/{2}x^2-2x$.
Donc : $g'(x)={1}/{3}3x^2+{1}/{2}2x-2=x^2+x-2$.
On a là un trinôme du second degré, de racines (évidentes) 1 et $-2$, de coefficient dominant $a=1$ strictement positif.
D'où le tableau qui suit.
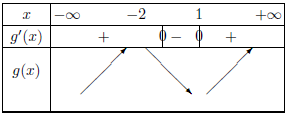
2. On constate que $g$ est strictement croissante à partir de $1$.
Et comme $u_n=g(n)$ pour $n≥1$, la suite
$(u_n)$ est strictement croissante.
3. La suite $(t_n)$ est définie pour $n≥0$.
On a: $t_0=g(0)=0$ et $t_1=g(1)={1}/{3}+{1}/{2}-2=={2}/{6}+{3}/{6}-{12}/{6}=-{7}/{6}$.
Donc $t_0>t_1$. Notons que cela se constate sans calcul grâce au tableau précédent
Finalement la suite $(t_n)$ n'est pas croissante!
Partie 2
1. On calcule: $x_B-x_A=0-2=-2$ $y_B-y_A=3-(-1)=4$
Donc on a: ${AB}↖{→}(-2\,;\,4)$
De même, on obtient: ${AC}↖{→}(1\,;\,2)$
Dans le repère orthonormé, on calcule alors: ${AB}↖{→}.{AC}↖{→}=-2×1+4×2$
Soit: ${AB}↖{→}.{AC}↖{→}=6$. c.q.f.d.
2. Dans le repère orthonormé, on calcule: $AB=√{(-2)^2+4^2}$. Soit: $AB=√{20}$
De même, on obtient: $AC=√{5}$.
3. On sait que: ${AB}↖{→}.{AC}↖{→}=AB×AC×\cos A↖{∧}$
Soit: $6=√{20}×√{5}×\cos A↖{∧}$
Et par là: $\cos A↖{∧}={6}/{√{20×5}}={6}/{√{100}}={6}/{10}=0,60$
Comme $\cos52^°≈0,62$, $\cos53^°≈0,60$ et $\cos54^°≈0,59$, on obtient alors: $A↖{∧}≈53^°$ au degré près.
4. Le vecteur ${1}/{2}.{AB}↖{→}$, de coordonnées $(-1\,;\,2)$, est directeur de la droite $(AB)$.
On pose: $-b=-1$ et $a=2$, soit: $b=1$ et $a=2$.
Donc une équation de (AB) est du type: $2x+y+c=0$.
Or, comme $B(0 \,;\, 3)$ est sur (AB), on a: $2×0+3+c=0$.
Et par là: $c=-3$
Donc une équation cartésienne de la droite (AB) est effectivement: $2x+y-3=0$. c.q.f.d.
Autre méthode
On note que: $2x_A+y_A-3=2×2+(-1)-3=0$, et par là, le point A est sur la droite d'équation $2x+y-3=0$.
De même: $2x_B+y_B-3=2×0+3-3=0$, et par là, le point B est sur la droite d'équation $2x+y-3=0$.
Par conséquent, la droite d'équation cartésienne $2x+y-3=0$ est la droite (AB). c.q.f.d.
5. Soit $d$ la hauteur du triangle ABC issue du sommet C.
$d$ a pour vecteur normal ${AB}↖{→}(-2\,;\,4)$
Donc une équation de $d$ est du type: $-2x+4y+c=0$.
Or, comme $C(3 \,;\, 1)$ est sur $d$, on a: $-2×3+4×1+c=0$.
Et par là: $c=2$
Donc une équation cartésienne de la droite $d$ est: $-2x+4y+2=0$.
Attention ! On peut alors remarquer que la hauteur $d$ a pour vecteur directeur ${u}↖{→}(-4;-2)$. Or le vecteur ${CH}↖{→}$ est aussi un vecteur directeur de la hauteur $d$,
mais il n'est pas forcément égal à ${u}↖{→}$ (on le voit à la fin). Les 2 vecteurs sont seulement colinéaires...
Le point H, pied la hauteur du triangle ABC issue du sommet C, appartient à $d$ et à (AB).
Donc ses coordonnées vérifient le système:
$\{\table -2x+4y+2=0; 2x+y-3=0$
Nous allons procéder par combinaisons linéaires.
$\{\table -2x+4y+2=0\;\;\;(L_1); 2x+y-3=0\;\;\;(L_2)$ $⇔$ $\{\table -2x+4y+2=0\;\;\; (L_1); -2x+4y+2+2x+y-3=0+0\;\;\; (L_1+L_2 ⇨L_2)$
$⇔$ $\{\table -2x+4y+2=0\;\;\; (L_1); 5y-1=0 \;\;\;(L_2)$
$⇔$ $\{\table -2x+4y+2=0; y={1}/{5}=0.2$
$⇔$ $\{\table -2x+4×0.2+2=0 ; y=0.2 $
$⇔$ $\{\table x={-2.8}/{-2}=1.4 ; y=0.2 $
Donc la solution du système est le couple $(x;y)=(\, 1,4\, ;\, 0,2\, )$.
Finalement, le point H a pour coordonnées $(\, 1,4\, ;\, 0,2\, )$.
Remarque: on obtient facilement ${CH}↖{→}(−1, 6;−0, 8)$. Ce vecteur est effectivement colinéaire au vecteur de coordonéees ${u}↖{→}(−4;−2)$,
mais les deux vecteurs ne sont pas égaux.
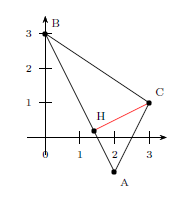
6.a. Soit $C$ le cercle de diamètre [BC].
Soit $M(x;y)$. On a alors: ${BM}↖{→}(x;y-3)$ et ${CM}↖{→}(x-3;y-1)$.
$M(x;y)$ est sur $C$ $ ⇔$ ${BM}↖{→}.{CM}↖{→}=0$.
$M(x;y)$ est sur $C$ $ ⇔$ $x(x-3)+(y-3)(y-1)=0$.
$M(x;y)$ est sur $C$ $ ⇔$ $x^2-3x+y^2-y-3y+3=0$.
$M(x;y)$ est sur $C$ $ ⇔$ $x^2-3x+y^2-4y+3=0$.
Ceci est bien l'équation de $C$ proposée. c.q.f.d.
Autre méthode
Soit K le milieu de [BC].
$x_K={x_B+x_C}/{2}={0+3}/{2}=1,5$ $y_K={y_B+y_C}/{2}={3+1}/{2}=2$
Donc on obtient: $K(1,5\,;\,2)$
On obtient alors: ${KB}↖{→}(-1,5\,;\,1)$
On calcule le rayon: $KB=√{(-1,5)^2+1^2}=√{2,25+1}=√{3,25}$.
Par ailleurs, on obtient: ${KM}↖{→}(x-1,5\,;\,y-2)$
Or : $M(x;y)$ est sur $C$ $ ⇔$ $KM^2=KB^2$.
$ ⇔$ $(x-1,5)^2+(y-2)^2=3,25$.
$ ⇔$ $x^2-3x+2,25+y^2-4y+4=3,25$.
$ ⇔$ $x^2-3x+y^2-4y+3=0$.
Ceci est bien l'équation de $C$ proposée. c.q.f.d.
6.b. Comme H est le pied la hauteur du triangle ABC issue du sommet C, le triangle BCH est rectangle en H, et par là, le point H appartient au cercle de diamètre [BC].
Autre méthode
Le cercle de diamètre [BC]a pour équation $x^2-3x+y^2-4y+3=0$.
On calcule: ${x_H}^2-3x_H+{y_H}^2-4y_H+3=1,4^2-3×1,4+0,2^2-4×0,2+3=1,96-4,2+0,04-0,8+3=2+3-5=0$
Et donc le point H appartient au cercle de diamètre [BC].