Variables aléatoires
Exercice 1
Un joueur utilise une machine à sous, appelée ARNAK, qui fonctionne de la façon suivante.
Le joueur mise 1 euro.
3 cas se présentent: soit le joueur perd sa mise, soit il la récupère, soit il gagne 100 euros (ce qui correspond à un gain algébrique de 99 euros).
La probabilité que le joueur perde est égale à 0,7.
La probabilité qu'il récupère son euro vaut $a$.
La probabilité qu'il gagne 100 euros vaut $b$.
1.a. Soit $X$ le gain algébrique du joueur.
Donner la loi de X.
Donner l'expression de son espérance en fonction de $a$ et $b$.
Déterminer $a$ et $b$ pour que, en moyenne, sur un grand nombre de parties, le joueur s'attende à perdre $0,5$ euro par partie.
1.b. Que vaut alors l'écart-type $σ$ de la variable aléatoire X?
1.c. Comparer cette machine ARNAK à la machine BANDYMANCHO, pour laquelle l'espérance de gain d'un joueur est de $-0,48$ euro par partie, et l'écart-type
associé s'élève à 9,87 euros.
2. 
Le joueur fait deux parties sur la machine ARNAK.
Soit Y son gain algébrique sur deux parties.
Déterminer la loi de Y ainsi que son espérance.
Corrigé
1.a. On a: $X(Ω)=\{-1;0;99\}$.
On a alors: $p(X=-1)=0,7$ et $p(X=0)=a$ et $p(X=99)=b$.
L'espérance de X vaut : $E(X)=0,7×(-1)+a×0+b×99=$$99b-0,7$.
D'autre part, en moyenne, sur un grand nombre de parties, le joueur s'attend à perdre $0,5$ euro par partie.
Par conséquent, l'espérance de X vaut également $-0,5$ euros.
On a donc: $99b-0,7=-0,5$
Et par là: $b={-0,5+0,7}/{99}={1}/{495}≈0,0020$
Par ailleurs, on sait que: $p(X=-1)+p(X=0)+p(X=99)=1$
Soit: $0,7+a+b=1$ (2).
Et par là: $a=0,3-b$.
Soit: $a=0,3-{1}/{495}={295}/{990}≈0,2980$.
Finalement: $b={1}/{495}≈0,002$ et $a={295}/{990}≈0,298$.
1.b. Première méthode:
Comme $E(X)=-0,5$, la variance V de X vaut:
$V=p(X=-1)×(-1+0,5)^2+p(X=0)×(0+0,5)^2+p(X=99)×(99+0,5)^2$
Soit: $V=0,7×(-1+0,5)^2+{295}/{990}×(0+0,5)^2+{1}/{495}×(99+0,5)^2$
Soit: $V=0,7×0,5^2+{295}/{990}×0,5^2+{1}/{495}×99,5^2$
Soit: $V=20,25$
Donc: $σ=√V=√{20,25}=$$4,5$.
Autre méthode:
Par application du Théorème de König-Huygens (à la limite du programme), on obtient:
$V=p(X=-1)×(-1)^2+p(X=0)×0^2+p(X=99)×99^2-(E(X))^2$
Soit: $V=0,7×1+{295}/{990}×0+{1}/{495}×9801-(-0,5)^2=0,7+19,8-0,25=20,25$
Donc: $σ=√V=√{20,25}=$$4,5$.
Cela est plus rapide que la première méthode!
Troisième méthode:
En utilisant sa calculatrice en mode STATISTIQUES, on rentre dans la Liste 1 les valeurs prises par X, et dans la liste 2 les probabilités associées.
La moyenne affichée est l'espérance de X. L'écart-type affiché est celui de X.
1.c. En moyenne, sur un grand nombre de parties, un joueur s'attend à perdre 0,5 euros par partie sur la machine ARNAK, et 0,48 euros par partie sur la machine
BANDYMANCHO.
Les pertes moyennes attendues sont proches.
Notons que, dans tous les cas, le joueur est perdant!
Par ailleurs, l'écart-type lié à la machine ARNAK est deux fois plus petit que celui lié à la machine BANDYMANCHO.
Par conséquent, le risque que le gain (ou la perte) soit loin de l'espérance est moins important pour la machine ARNAK.
2. Les deux parties sont indépendantes. Pour chacune d'elle, il y a
trois éventualités:
$X=-1$, $X=0$ et $X=99$, dont les probabilités sont:
$p(X=-1)=0,7$, $p(X=0)≈0,298$ et $p(X=99)≈0,002$.
On peut construire l'arbre de probabilités suivant:
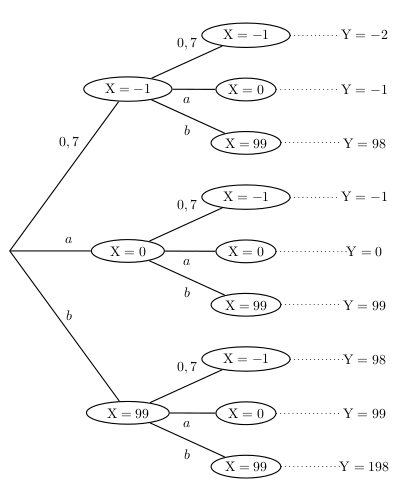
La probabilité d'une liste de résultats est le produit des probabilités de ces résultats.
On obtient alors:
$p(Y=-2)=0,7×0,7=0,49$
$p(Y=-1)=0,7×a+a×0,7=1,4×{295}/{990}={413}/{990}≈0,42$
$p(Y=0)=a×a={295^2}/{990^2}={87025}/{980100}≈0,089$
$p(Y=98)=0,7×b+b×0,7≈1,4×{1}/{495}={14}/{4950}≈0,0028$
$p(Y=99)=a×b+b×a={590}/{490050}≈0,0012$
$p(Y=198)=b×b={1}/{245025}≈0,0000041$
L'espérance de Y vérifie l'égalité:
$E(Y)=p(Y=-2)×(-2)+p(Y=-1)×(-1)+p(Y=0)×0+p(Y=98)×98+p(Y=99)×99+p(Y=198)×198$
Soit: $ E(Y)=0,49×(-2)+{413}/{990}×(-1)+{87025}/{980100}×0+{14}/{4950}×98+{590}/{490050}×99+{1}/{245025}×198$
Soit: $ E(Y)=-1$
En moyenne, sur un grand nombre de parties doubles, le joueur peut espérer perdre $1$ euro par partie double.
Autre méthode: on utilise la linéarité de l'espérance (mais ce concept est hors programme)...
On constate que: $Y=X+X=2X$, et par là, on obtient: $E(Y)=E(2X)$
Et, par linéarité, on a finalement: $E(Y)=2E(X)=2×(-0,5)=-1$