 Variables aléatoires
Variables aléatoires
Exercice 2
Une urne contient $n$ boules.
Une boule est rouge. 5 boules sont blanches. Les autres sont noires.
Un joueur prélève deux fois de suite une boule de l'urne, avec remise de la première boule dans l'urne.
Si les 2 boules tirées sont noires, ou si le tirage contient une noire et une rouge, alors le joueur gagne $190$ euros, sinon, il perd $60$ euros.
Déterminer $n$ pour que le jeu soit équitable.
Un jeu est équitable si et seulement si l'espérance de gain du joueur est nulle.
Corrigé
Remarquons pour commencer que, s'il existe, $n$ est un entier naturel au moins égal à 6.
Pour chaque tirage: $p(R)={1}/{n}$ $p(N)={n-6}/{n}$ $p(B)={5}/{n}$
Les tirages sont indépendants.
Nous pouvons dresser l'arbre de probabilités suivant.
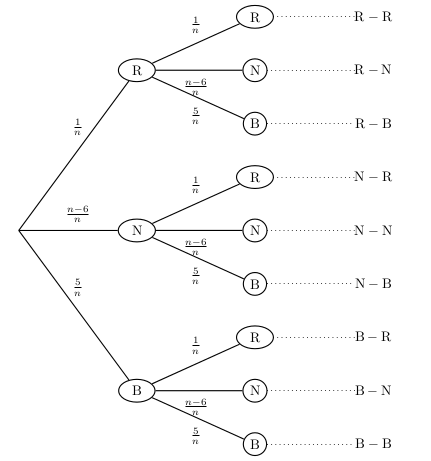
La probabilité d'une liste de résultats est le produit des probabilités de ces résultats.
On obtient ainsi: $p(N-N)={n-6}/{n}×{n-6}/{n}={n^2-12n+36}/{n^2}$
$p(R-N)+p(N-R)={1}/{n}×{n-6}/{n}+{n-6}/{n}×{1}/{n}={2n-12}/{n^2}$
Soit X est la variable aléatoire représentant le gain du joueur. On a alors:
$p(X=190)=p(N-N)+p(R-N)+p(N-R)$
Donc: $p(X=190)={n^2-12n+36}/{n^2}+{2n-12}/{n^2}={n^2-10n+24}/{n^2}$
$p(X=-60)=1-p(X=190)={10n-24}/{n^2}$
Le jeu est équitable si et seulement si $E(X)=0$.
Or $E(x)=p(X=190)×190+p(X=-60)×(-60)=190{n^2-10n+24}/{n^2}-60{10n-24}/{n^2}$.
Par conséquent, on résout: ${190n^2-1900n+4560}/{n^2}-{600n-1440}/{n^2}=0$ $⇔$ ${190n^2-2500n+6000}/{n^2}=0$
Un quotient est nul si et seulement si son numérateur est nul.
On cherche donc les racines du trinôme $190n^2-2500n+6000$.
$a=190$; $b=-2500$; $c=6000$. $Δ=1690000$
$Δ>0$ Le trinôme a 2 racines:
$n_1={2500-√{1690000}}/{380}≈3,16$ et $n_2={2500+√{1690000}}/{380}=10$.
Une seule des racines est un entier naturel au moins égal à 6; c'est $n_2$.
Finalement, le jeu est équitable si l'urne contient 10 boules.