 Variables aléatoires
Variables aléatoires
Exercice 3
Une société assure annuellement les téléviseurs d'une chaîne hôtelière de luxe. Chaque téléviseur est assuré pour 40 euros.
Le risque qu'un problème mineur survienne dans l'année est de $10\%$. Le coût du sinistre pour l'assureur est alors de 120 euros (en moyenne).
Le risque qu'un problème majeur survienne dans l'année est de $2\%$. Le coût du sinistre pour l'assureur est alors de 1020 euros (en moyenne).
Soit X la variable aléatoire donnant le gain algébrique annuel de l'assureur par contrat pour un téléviseur.
Les valeurs prises par X sont donc $40$, $-80$ et $-980$.
- Donner la loi de X.
- Combien l'assureur peut-il espérer gagner en moyenne par contrat?
 On considère le programme en Python ci-dessous.
On considère le programme en Python ci-dessous.
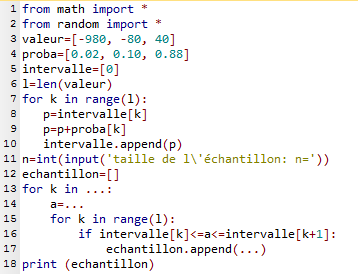
Expliquer comment fonctionne la boucle des lignes 7 à 10.
Vérifier qu'après exécution de cette boucle, la liste intervalle est égale à [0, 0.02, 0.12, 1] Compléter le programme précédent pour qu'il simule des valeurs prises par X pour un
échantillon de $n$ contrats.
Compléter le programme précédent pour qu'il simule des valeurs prises par X pour un
échantillon de $n$ contrats.
 On a complété le programme précédent en ajoutant les lignes 19 à 23.
On a complété le programme précédent en ajoutant les lignes 19 à 23.
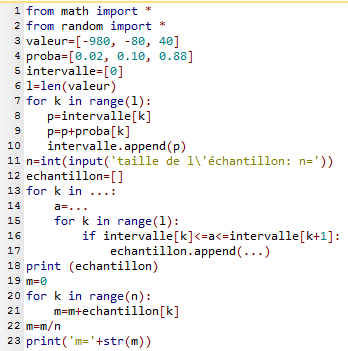
A quoi sert le programme ci-dessus?- Faite fonctionner ce programme pour des grandes valeurs de n (par exemple n=10 000).
Vers quelle valeur tend certainement la valeur de m?
Corrigé
- On a: $X(Ω)=\{-80;-980;40\}$.
On a alors: $p(X=-80)=0,10$ et $p(X=-980)=0,02$ et $p(X=40)=1-0,10-0,02=0,88$.
- L'espérance de X vaut : $E(X)=0,10×(-80)+0,02×(-980)+0,88×40=7,60$.
Donc, en moyenne, sur un grand nombre de contrats, l'assureur peut espérer gagner 7,60 euros par contrat.  Fonctionnement de la boucle des lignes 7 à 10
Fonctionnement de la boucle des lignes 7 à 10
l est la longueur de la liste valeur; l vaut 3.
k va donc varier de 0 à 2
Pour k=0, on obtient:
p=intervalle[0]=0
p=p+proba[0]=0+0.02=0.02
intervalle=[0, 0.02]
Pour k=1, on obtient:
p=intervalle[1]=0.02
p=p+proba[1]=0.02+0.10=0.12
intervalle=[0, 0.02, 0.12]
Pour k=2, on obtient:
p=intervalle[2]=0.12
p=p+proba[2]=0.12+0.88=1
intervalle=[0, 0.02, 0.12, 1]
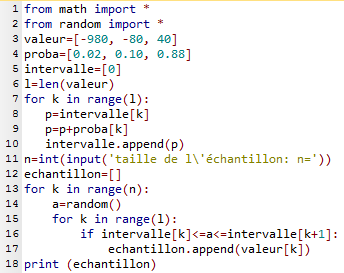
Après exécution de la boucle, la liste intervalle est bien égale à [0, 0.02, 0.12, 1] Voici le programme complété pour qu'il simule des valeurs prises par X pour un
échantillon de $n$ contrats.
Voici le programme complété pour qu'il simule des valeurs prises par X pour un
échantillon de $n$ contrats.
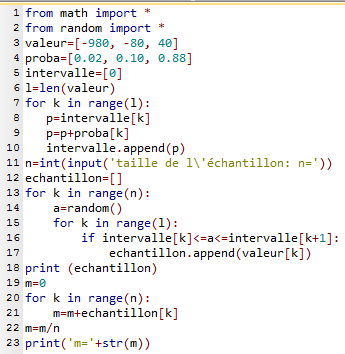
 Le programme ci-dessous permet de déterminer la valeur moyenne de X pour un échantillon
de $n$ contrats.
Le programme ci-dessous permet de déterminer la valeur moyenne de X pour un échantillon
de $n$ contrats.
- Quand n devient grand, la probabilité que m soit loin de l'espérance de X, égale à 7,60, est de plus en plus faible. Cela se vérifie en faisant fonctionner ce le programme pour des grandes valeurs de n.