Fonction exponentielle
Fonction exponentielle
Exercice 6
Soit $f$ la fonction définie sur l’intervalle $[0;30]$ par $f(x)=5+xe^{-0,2x+1}$.
Soit $\C_f$ la courbe représentative de $f$.
- Soit $f\,'$ la fonction dérivée de la fonction $f$.
Montrer que,pour tout réel $x$ de l’intervalle $[0;30]$, $f\,'(x)=(-0,2x+1)e^{-0,2x+1}$. - En déduire le tableau de variation de $f$ sur l’intervalle $[0;30]$.
- On considère l'équation $f(x)=7$ sur l'intervalle $[0; 5]$.
Compte tenu du tableau de variation précédent, on admet que cette équation admet une solution unique $α$ dans l’intervalle $[0; 5]$.
Déterminer par essais successifs une valeur de $α$ arrondie à 0,1 près. - Montrer que la tangente $t$ à $\C_f$ en 10 admet pour équation $y=-{1}/{e}x+5+{20}/{e}$.
- Recopier et compléter le tableau suivant (où les valeurs seront arrondies à 0,1 près).

Puis tracer $\C_f$ et $t$.
On placera également le point A de $\C_f$ d'abscisse 10 sur le graphique.
On vérifiera graphiquement que la valeur $α$ semble convenir.
Corrigé
- On pose: $u=x$ et $a=-0,2$ et $b=1$. On a donc: $u\,'=1$.
Ici: $f=5+ue^{ax+b}$, et donc: $f\,'=0+u'×e^{ax+b}+u×a×e^{ax+b}$.
Donc, pour tout réel $x$ de l’intervalle $[0;30]$, on a:
$f\,'(x)=1×e^{-0,2x+1}+x×(-0,2)×e^{-0,2x+1}$.
Soit: $f\,'(x)=e^{-0,2x+1}(1-x×0,2)$.
Soit: $f\,'(x)=(-0,2x+1)e^{-0,2x+1}$. - Une exponentielle est strictement positive. Donc $f\,'(x)$ est du signe de $-0,2x+1$.
Cette fonction affine, de coefficient directeur -0,2 strictement négatif, s'annule pour $x={-1}/{-0,2}=5$.
D'où le tableau de variation de $f$ sur l’intervalle $[0;30]$.
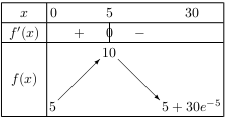
- On cherche $α$ par essais successifs.
Dans le tableau suivant, les valeurs sont arrondies à 0,01 près.

Par conséquent, $α$ est compris entre 0,85 et 0,9.
D'où $α≈0,9$ (arrondi à 0,1 près) - La tangente $t$ à $\C_f$ en 10 admet pour équation $y=f(10)+f\,'(10)(x-10)$.
Or on a: $f(10)=5+10e^{-1}=5+{10}/{e}$ et $f\,'(10)=(-0,2×10+1)e^{-0,2×10+1}=-e^{-1}=-{1}/{e}$.
Donc $t$ a pour équation $y=5+{10}/{e}+(-{1}/{e})(x-10)$.
Soit: $y=5+{10}/{e}-{1}/{e}x+{10}/{e}$.
Soit: $y=-{1}/{e}x+5+{20}/{e}$.
- Tableau de valeurs:
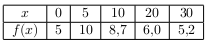
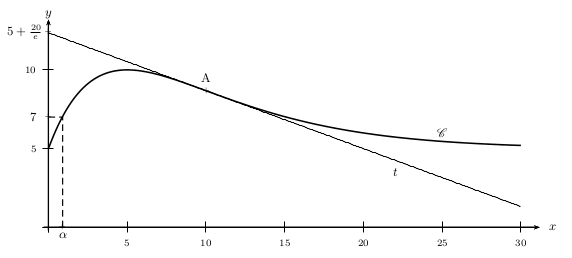
Ci-dessous le graphique demandé.
On notera que $t$ passe par A et a pour ordonnée à l'origine $5+{20}/{e}≈12,4$.
Par ailleurs, $α$ semble bien être l'unique antécédent de 7 sur l'intervalle $\[0;5\]$.