 Probabilités conditionnelles
Probabilités conditionnelles
Exercice 1
Un courtier en assurance propose 3 contrats:
- Responsabilité civile
- Véhicule
- Habitation
Ses 1000 clients ont tous souscrit le contrat Responsabilité civile. Parmi ceux-là, 800 ont souscrit le contrat Véhicule,
700 ont souscrit le contrat Habitation et 650 ont soucrit à la fois le contrat Véhicule et le contrat Habitation.
Le courtier sort le dossier d'un client au hasard.
Soit V: "le client a souscrit le contrat Véhicule".
Soit H: "le client a souscrit le contrat Habitation".
Soit E:" "le client a souscrit uniquement le contrat Responsabilité civile".
- Déterminer $p(V)$ et $p(H)$.
- Décrire par une phrase chacun des évènements: $V∩H$ et $V∪H$.
- Déterminer la probabilité de chacun des évènements $V∩H$ et $V∪H$.
- Déterminer $p(E)$.
- En lisant la première ligne du contrat, le courtier comprend que le client a souscrit le contrat Véhicule.
Quelle est la probabilité que le client ait souscrit le contrat Habitation?
Corrigé
-
$\text"Card Ω"=1000$. Il y a équiprobabilité.
Les 1000 issues de l'expérience sont décrites par le diagramme ci-contre.
L'univers est l'intérieur de la grande ellipse.
V est la zone rose ou violine.
H est la zone bleue ou violine.
$V∩H$ est la zone violine.
E est la zone jaune.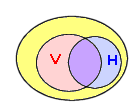
$\text"Card V"=800$. Donc: $p(V)={800}/{1000}=0,80$.
$\text"Card H"=700$. Donc: $p(H)={700}/{1000}=0,70$.
- $V∩H$: "le client a souscrit le contrat Véhicule et le contrat Habitation".
$V∪H$: "le client a souscrit le contrat Véhicule ou le contrat Habitation (ou les 2)". - $\text"Card Ω"=1000$. Il y a équiprobabilité.
$\text"Card V∩H"=650$. Donc: $p(V∩H)={650}/{1000}=0,65$.
$p(V∪H)=p(V)+p(H)-p(V∩H)=0,80+0,70-0,65=0,85$. - E est l'évènement contraire de $V∪H$.
$p(E)=1-p(V∪H)=1-0,85=0,15$. - En lisant la première ligne du contrat, le courtier comprend que le client a souscrit le contrat Véhicule".
L'univers se réduit donc aux 800 issues de V, qui sont équiprobables.
Parmi celles-ci, 650 issues sont favorables.
Donc la probabilité cherchée est ${650}/{800}=0,8125$.
Autre méthode.
On cherche: $p_V(H)={p(H∩V)}/{p(V)}={0,65}/{0,80}=0,8125$.