Probabilités conditionnelles
Exercice 3
Une urne contient 1000 jetons numérotés, dont 600 rouges et 400 noirs. 20% des jetons noirs portent un numéro pair.
On tire un jeton de l'urne.
Soit R: "le jeton tiré est rouge ".
Soit N: "le jeton tiré est noir ".
Soit P: "le jeton tiré porte un numéro pair".
- On sait que la probabilité que le jeton tiré porte un numéro pair vaut 0,26.
Quelle est la probabilité que le jeton tiré soit rouge et porte un numéro pair? - On sait que le jeton tiré porte un numéro pair.
Quelle est la probabilité (arrondie à 0,01 près) que le jeton tiré soit rouge?
Corrigé
- Arbre pondéré décrivant l'expérience .
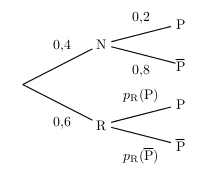
$\{N;R\}$ constitue une partition de l'univers.
On sait que $p(P)=p(N∩P)+p(R∩P)$ (par application de la formule des probabilités totales).
Soit: $0,26=p(N)×p_N(P)+p(R∩P)$ (par application de la règle du produit).
Soit: $0,26=0,4×0,2+p(R∩P)$.
Et par là: $0,26-0,08=p(R∩P)$.
Soit: $p(R∩P)=0,18$. C'est la probabilité cherchée. - La probabilité cherchée est: $p_{P}(R)={p(R∩P)}/{p(P)}={0,18}/{0,26}≈0,69$.