Probabilités conditionnelles
Exercice 4
Dans une usine, l'ingénieur qualité teste la conformité des objets produits par ses deux robots.
10% des objets sont assemblés par le robot A; les autres sont assemblés par le robot B.
Le robot A, très usagé, produit 20% d'objets non conformes.
Le robot B, plus récent, produit 3% d'objets non conformes.
L'ingénieur prélève au hasard un objet fabriqué dans la journée.
Soit NC: "l'objet est non conforme ".
Soit C: "l'objet est conforme ".
Soit A: "l'objet a été fabriqué par le robot A".
Soit B: "l'objet a été fabriqué par le robot B".
- Déterminer la probabilité que l'objet soit non conforme.
- Déterminer la probabilité que l'objet ait été fabriqué par le robot A sachant qu'il est non conforme.
Corrigé
-
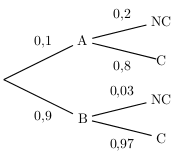
Nous pouvons dresser un arbre pondéré décrivant l'expérience .
- $\{A;B\}$ constitue une partition de l'univers.
La probabilité cherchée est alors: $p(NC)=p(A∩NC)+p(B∩NC)$ (par application de la formule des probabilités totales).
Soit: $p(NC)=p(A)×p_A(NC)+p(B)×p_B(NC)$
Soit: $p(NC)=0,10×0,20+0,90×0,03=0,02+0,027=0,047$. - La probabilité cherchée est $p_{NC}(A)={p(NC∩A)}/{p(NC)}={0,02}/{0,047}≈0,43$.
