Probabilités conditionnelles
Exercice 5
Dans cet exercice, toute trace de recherche serait prise en compte pour la notation.
Pour garantir l'anonymat dans certaines enquêtes, on introduit parfois le hasard dans les réponses possibles.
Inquiet devant l'apathie en cours d'un nombre important de ses élèves,
le proviseur d'un lycée se demande quelle est la proportion d'élèves qui fument régulièrement du cannabis.
Il veut interroger lui même chaque élève, mais il craint que la plupart ne lui mentent.
Il interroge donc les élèves selon un protocole particulier.
En effet, il demande à chaque élève de se retirer dans un isoloir et de jouer à pile ou face.
S'il obtient pile, il doit répondre honnêtement par Oui ou par Non à la question : "fumez vous régulièrement du cannabis ?"
S'il obtient face, il doit rejouer à pile ou face et répondre par Oui ou par Non à la question : "avez vous obtenu Face la seconde fois ?"
Quand l'élève sort de l'isoloir, le seul mot qu'il échange avec le proviseur est "Oui" ou "Non". Il est donc protégé car le proviseur
ne sait pas à quelle question il répond, et cela réduit au maximum les non-réponses et les fausses réponses.
Dans ce qui suit, on supposera donc que les réponses des sondés sont honnêtes.
Le proviseur a récolté 35% de "Oui".
Soit P l'événement: "le premier lancer de la pièce donne Pile".
Soit O l'événement: "l'élève répond Oui au proviseur".
Soit $p$ la probabilité pour qu'un élève sondé fume régulièrement du cannabis.
-
Dresser un arbre pondéré décrivant l'expérience.
-
Déterminer la probabilité $p$. - Le proviseur croise un élève ayant répondu "Oui" à l'enquête. Quelle est la probabilité (arrondie à 0,01) que cet élève fume régulièrement du cannabis?
Dans cette question, on pourra considérer l'évènement C: "l'élève fume régulièrement du cannabis", pour un élève pris au hasard dans l'établissement.
Corrigé
- Voici quelques explications sur la façon de compléter correctement l'arbre de probabilités.
Supposons que l'élève obtienne Pile au premier lancer.
La probabilité qu'il réponde alors Oui à la question : "fumez-vous régulièrement du cannabis ?" est $p$ (car l'élève est supposé ne pas mentir).
On notera que l'évènement "l'élève fume régulièrement du cannabis" est indépendant du fait qu'il ait obtenu Pile au lancer de la pièce.
On a: $p_P(O)=p($"l'élève fume régulièrement du cannabis"$)=p$
Supposons que l'élève obtienne Face au premier lancer.
La probabilité qu'il obtienne alors Face au second lancer est 0,5, et par là, la probabilité qu'il réponde Oui à l'enquêteur est aussi égale à 0,5.
Soit F l'événement: "le premier lancer de la pièce donne Face".
Soit N l'événement: "l'élève répond Non à l'enquêteur".
Voici alors un arbre pondéré décrivant l'expérience .
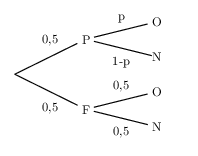
- $\{P;F\}$ constitue une partition de l'univers.
On sait que $p(O)=p(P∩O)+p(F∩O)$ (par application de la formule des probabilités totales).
Soit: $0,35=p(P)×p_P(O)+p(F)×p_F(O)$ (par application de la règle du produit).
Soit: $0,35=0,5×p+0,5×0,5$.
Et par là: $0,35-0,25=0,5×p$.
Et donc: $p={0,10}/{0,5}=0,20$.
On notera que, si les réponses des sondés étaient honnêtes, alors la conclusion de l'enquête serait que $20\%$ des élèves du lycée fument régulièrement du cannabis. - On cherche ici à déterminer la valeur de $p_O(C)$.
On a: $p_O(C)={p(O∩C)}/{p(O)}$
Méthode 1
On a: $p_O(C)={p(C)×p_C(O)}/{p(O)}$
On sait que: $p(C)=0,20$ et que: $p(O)=0,35$.
Par ailleurs: $p_C(O)=1-p_C(N)$. Or, si l'élève a répondu Non sachant qu'il fume du cannabis, c'est qu'il avait obtenu Face au premier lancer, puis Pile au second lancer (pour répondre Non). Donc $p_C(N)=p(F∩N)$, et donc: $p_C(O)=1-p(F∩N)=1-0,5×0,5=0,75$.
Donc finalement, on obtient: $p_O(C)={0,20×0,75}/{0,35}$
Soit: $p_O(C)≈0,43$
Méthode 2
$\{P;F\}$ constitue une partition de l'univers.
On sait que $p(O∩C)=p(P∩O∩C)+p(F∩O∩C)$ (par application de la formule des probabilités totales).
D'où: $p(O∩C)=p(C)×p_C(P)×p_{C∩P}(O)+p(C)×p_C(F)×p_{C∩F}(O)$
Soit: $p(O∩C)=0,2×0,5×1+0,2×0,5×0,5$
Soit: $p(O∩C)=0,15$
Et comme $p(O)=0,35$, on obtient: $p_O(C)={0,15}/{0,35}≈0,43$