 Probabilités conditionnelles
Probabilités conditionnelles
Exercice 6
Un exercice qui permet de se perfectionner en PYTHON, mais qui ne serait pas donné tel quel dans un devoir surveillé...
Le plan est rapporté au repère orthonormé (O,I,J).
Soit $\C$ le cercle de centre O et de rayon 1.
Soit A(1;1).
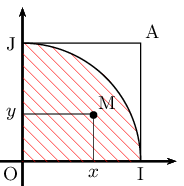
- Soit M un point de coordonnées $(x, y)$.
Exprimer la distance OM en fonction de $x$ et $y$. -
Soit $\D$ le quart de disque de centre O de rayon 1 situé dans le premier quadrant.
On suppose que $\D$ est privé des points I et J.
$\D$ est hachuré en rouge sur le graphique.
On considère un point M de coordonnées (x, y), avec $0≤x$<$1$ et $0≤y$<$1$.
Expliquer pourquoi le point M est dans $\D$ si et seulement si $x^2+y^2≤1$. -
Quelle est l'aire de $\D$?
Quelle est l'aire du carré OIAJ ?
- On tire aléatoirement les valeurs des nombres réels x et y dans l'intervalle $[0;1[$, puis on place le point M de coordonnées (x;y) sur le graphique.
Le point M est nécessairement dans le carré OIAJ.
Quelle est la probabilité que le point M appartienne à $\D$? - On répète $n$ fois de suite l'expérience précédente.
Soit $m$ le nombre de points dans $\D$.
Expliquer pourquoi, le rapport ${m}/{n}$ est certainement une approximation du nombre ${π}/{4}$ si le nombre de tirages $n$ est grand. - Compléter les lignes 12, 14, 15 et 18 du programme suivant, écrit en Python, pour qu'il permette de simuler les $n$ expériences ci-dessus, et qu'il affiche finalement la valeur de ${m}/{n}$
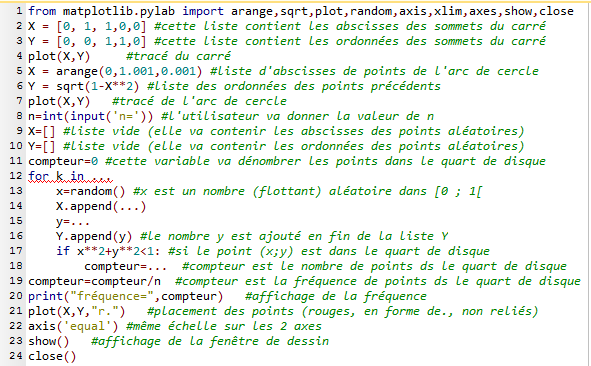
Toute phrase qui suit un dièse (#) est un commentaire.
Les instructions concernant l'affichage graphique et les entrées-sorties ne sont pas exigibles, c'est pourquoi elles sont toutes commentées. - Faire fonctionner le programme pour n=200.
- Faire fonctionner le programme pour n=10 000.
Donner la valeur de la fréquence obtenue arrondie à 0,01 près, et comparer à ${π}/{4}$. - On a adapté le programme pour qu'il permette d'obtenir une valeur approchée de l'aire du domaine hachuré sur le dessin suivant.
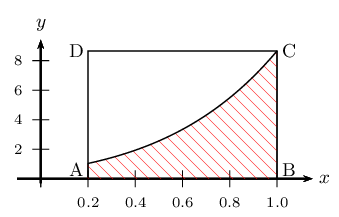
La fonction représentée ci-dessus est la fonction $f$ définie par $f(x)=(2x+x^2)exp(x)+0,5$ sur l'intervalle $[0,2;1]$.
Voici le programme.
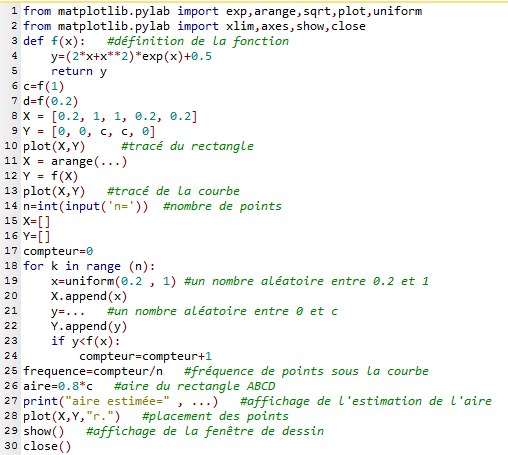
Compléter le programme proposé. Le faire fonctionner, et estimer l'aire.
Corrigé

- Soit M un point de coordonnées $(x, y)$.
On a: ${OM}↖{→}(x;y)$.
Et comme le repère est orthonormé, on obtient: $OM=√{x^2+y^2}$ -
Soit $\D$ le quart de disque de centre O de rayon 1, situé dans le premier quadrant, et privé des points I et J.
Un point M de coordonnées (x, y), où $0≤x$<$1$ et $0≤y$<$1$, est situé dans le carré OIAJ privé des bords [IA] et [AJ].
Comme $\D$ a pour rayon 1, un tel point M est dans $\D$ si et seulement si $OM≤1$,
c'est à dire: si et seulement si $OM^2≤1^2$ (car OM est positif
c'est à dire: si et seulement si $x^2+y^2≤1$. -
L'aire de $\D$ vaut $a_D={π×OM^2}/{4}={π×1^2}/{4}=$${π}/{4}$
L'aire du carré OIAJ vaut $a_C=OI^2=1^2=$$1$
- La probabilité que le point M appartienne à $\D$ vaut $p={a_D}/{a_C}={{π}/{4}}/{1}=$${π}/{4}$
- On répète $n$ fois de suite l'expérience citée.
Soit $f$ la fréquence des points M se retrouvant dans $\D$
Soit $p$ la probabilité qu'un point M appartienne à$\D$.
Et $f$ est certainement proche de $p$ si $n$ est suffisamment grand.
Or, comme $m$ est le nombre de points dans $\D$, on a: $f={m}/{n}$
Et par ailleurs, on a: $p={π}/{4}$.
Donc le rapport ${m}/{n}$ est certainement une approximation du nombre ${π}/{4}$ si le nombre de tirages $n$ est grand.
La méthode utilisée s'appelle la méthode de Monte Carlo. - Voici le programme complété pour qu'il permette de simuler les $n$ expériences ci-dessus, et qu'il affiche finalement la valeur de ${m}/{n}$
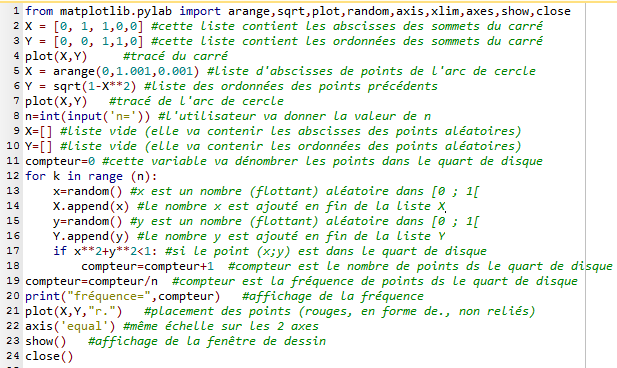
- Voici la fenêtre qui s'affiche pour n=200. Evidemment, le caractère aléatoire du placement des points vous donnera un graphique légèrement différent!
Attention! Il faut fermer la fenêtre pour que le programme se termine.
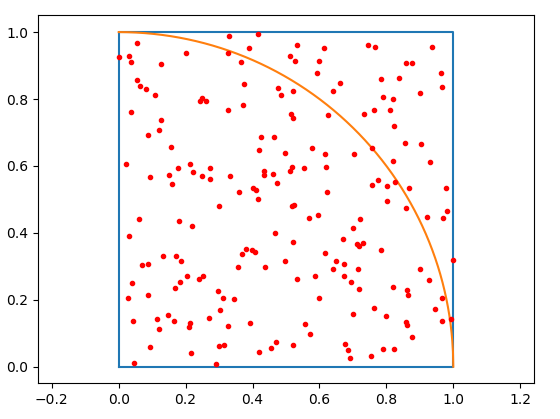
- Pour n=10 000, j'ai obtenu une fréquence de 0,79 arrondie à 0,01 près, très proche de ${π}/{4}$ qui vaut également environ 0,79 arrondi à 0,01 près.
- Voici le programme complété.
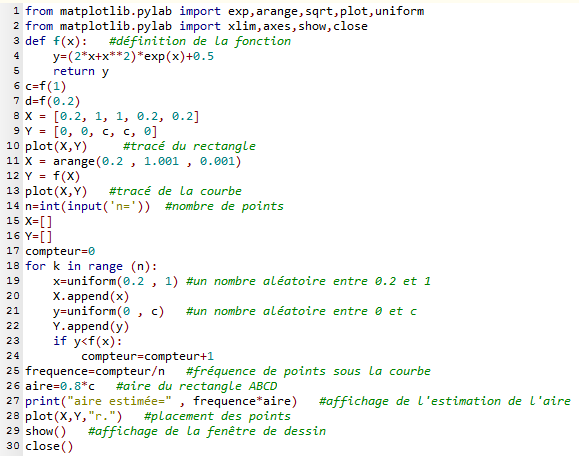
Pour n=10 000, j'ai obtenu une estimation de l'aire égale à 3,11 arrondie à 0,01 près, très proche de 3,07, trouvée par une autre méthode dans un exercice de niveau seconde.