Produit scalaire dans le plan
Exercice 1
Partie 1.
Soient $u↖{→}$ et $v↖{→}$ deux vecteurs d'angle géométrique $a$ (en radians) et soit $p$ leur produit sacalaire.
- Calculer $p$ si $∥u↖{→}∥=2$ , $∥v↖{→}∥=3$ et $a={π}/{6}$.
- Calculer $∥u↖{→}∥$ si $p=5$, $∥v↖{→}∥=10$ et $a={π}/{3}$.
- Déterminer une mesure de $a$ (en radians) si $∥u↖{→}∥=√2$ , $∥v↖{→}∥=8$ et $p=-8$.
Partie 2.
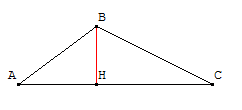
Soit ABC un triangle. Soit H le pied de la hauteur issue de B.
- Calculer ${AB}↖{→}.{AC}↖{→}$ si $AH=2$, $AC=5$ et H appartient au segment [AC].
- Calculer ${AB}↖{→}.{AC}↖{→}$ si $AH=3$, $AC=9$ et A appartient au segment [HC].
- Calculer AH si ${AB}↖{→}.{AC}↖{→}=7$ si $AC=5$.
Partie 3.
Soit ABC un triangle tel que $AB=c$, $BC=a$ et $CA=b$
-
Décomposer le vecteur ${AB}↖{→}$ à l'aide de la relation de Chasles,
puis démontrer que $c^2=a^2+b^2-2ab\cos C↖{∧}$ à l'aide du produit scalaire.
Quelle formule bien connue a-t-on redémontrée? - Calculer $c$ si $a=2$, $b=3$ et ${C}↖{∧}={π}/{3}$
- Déterminer une mesure de ${C}↖{∧}$ (arrondie au degré) si $a=2$, $b=3$ et $c=4$
Partie 4.
Le plan est rapporté au repère orthonormé $(O,I,J)$.
Soient $A(-1;2)$, $B(-3;1)$ et $C(1;-3)$ trois points.
- Calculer le produit scalaire ${AB}↖{→}.{AC}↖{→}$
- En déduire une mesure de ${A}↖{∧}$ (arrondie au degré)
Corrigé
Partie 1.
Soient $u↖{→}$ et $v↖{→}$ deux vecteurs d'angle géométrique $a$ (en radians) et soit $p$ leur produit sacalaire.
- On a: $p=∥u↖{→}∥×∥v↖{→}∥×\cos a=2×3×\cos {π}/{6}=6×{√3}/{2}=3√3$.
- On a: $p=∥u↖{→}∥×∥v↖{→}∥×\cos a$
Soit: $5=∥u↖{→}∥×10×\cos {π}/{3}$
Soit: $5=∥u↖{→}∥×10×0,5$
Et donc: $∥u↖{→}∥={5}/{5}=1$. - On a: $p=∥u↖{→}∥×∥v↖{→}∥×\cos a$
Soit: $-8=√2×8×\cos a$
Donc: $\cos a={-8}/{8√2}=-{√2}/{2}$
Par oonséquent, une mesure de $a$ est $π-{π}/{4}={3π}/{4}$.
Partie 2.
- On a: ${AB}↖{→}.{AC}↖{→}=AH×AC$ (car H, pied de la hauteur issue de B, appartient au segment [AC])
Donc: ${AB}↖{→}.{AC}↖{→}=2×5=10$
- On a: ${AB}↖{→}.{AC}↖{→}=-AH×AC$ (car H est le pied de la hauteur issue de B, et A appartient au segment [HC])
Donc: ${AB}↖{→}.{AC}↖{→}=-3×9=-27$
- comme H est le pied de la hauteur issue de B, on a:
soit: ${AB}↖{→}.{AC}↖{→}=-AH×AC$, soit ${AB}↖{→}.{AC}↖{→}=AH×AC$
Or: ${AB}↖{→}.{AC}↖{→}=7$.
Et ce produit scalaire est positif.
Donc nécessairement: ${AB}↖{→}.{AC}↖{→}=AH×AC$
Et on obtient donc: $7=AH×5$.
Et par là: $AH={7}/{5}=1,4$.
Partie 3.
Soit ABC un triangle tel que $AB=c$, $BC=a$ et $CA=b$
-
D'après la relation de Chasles, on a: ${AB}↖{→}={AC}↖{→}+{CB}↖{→}$
On calcule alors: $c^2={∥}{AB}↖{→}{∥^2}={AB}↖{→}.{AB}↖{→}$
On obtient donc: $c^2=({AC}↖{→}+{CB}↖{→}).({AC}↖{→}+{CB}↖{→})$
D'où: $c^2={AC}↖{→}.{AC}↖{→}+{AC}↖{→}.{CB}↖{→}+{CB}↖{→}.{AC}↖{→}+{CB}↖{→}.{CB}↖{→}$
Donc: $c^2={∥}{AC}↖{→}{∥}^2+2×({AC}↖{→}.{CB}↖{→})+{∥}{CB}↖{→}{∥}^2$
Soit: $c^2=b^2-2×({CA}↖{→}.{CB}↖{→})+a^2$
Et finalement: $c^2=a^2+b^2-2ab\cos C↖{∧}$.
On reconnait ici la "formule d'Al-Kashi".
- On a: $c^2=a^2+b^2-2ab\cos C↖{∧}$.
Soit: $c^2=2^2+3^2-2×2×3×\cos {π}/{3}$.
Soit: $c^2=4+9-12×\0,5=7$.
Et par là, comme $c$ est positif, on a: $c=√7$ - On a: $c^2=a^2+b^2-2ab\cos C↖{∧}$.
Soit: $4^2=2^2+3^2-2×2×3×\cos C↖{∧}$.
Donc: $16-4-9=-12×\cos C↖{∧}$.
Et par là: $\cos C↖{∧}={3}/{-12}=-0,25$
A l'aide de la calculatrice, on obtient alors une mesure de $a$, et on trouve: $a≈104°$ (arrondie au degré)
Partie 4.
Le plan est rapporté au repère orthonormé $(O,I,J)$.
Soient $A(-1;2)$, $B(-3;1)$ et $C(1;-3)$ trois points.
- On obtient: ${AB}↖{→}(x_B-x_A;y_B-y_A)=(-3+1;1-2)=(-2;-1)$
De même, on obtient: ${AC}↖{→}(2;-5)$
Le repère étant orthonormé, on a: ${AB}↖{→}.{AC}↖{→}=(-2)×2+(-1)×(-5)=1$ - On sait que: ${AB}↖{→}.{AC}↖{→}= AB×AC×\cos A↖{∧}$
Donc: $1= AB×AC×\cos A↖{∧}$
Or: $AB={∥}{AB}↖{→}{∥}=√{(-2)^2+(-1)^2}=√{5}$
Et: $AC={∥}{AC}↖{→}{∥}=√{2^2+(-5)^2}=√{29}$
Donc: $1= √{5}×√{29}×\cos A↖{∧}$
Et par là: $\cos A↖{∧}={1}/{√{145}}$
A l'aide de la calculatrice, on obtient alors une mesure de $A↖{∧}$, et on trouve: $A↖{∧}≈85°$ (arrondie au degré)