Produit scalaire dans le plan
Exercice 2
Un exercie pour apprendre à utiliser les 4 formes du produit scalaire....
Soient A, B et C trois points et D le projeté orthogonal de B sur (AC).
On suppose que: BD=4, CD=2 et AC=3.
Par ailleurs, C appartient au segment [AD].
Nous allons déterminer le produit scalaire ${BA}↖{→}.{BC}↖{→}$ de quatre façons différentes.
Méthode 1
1. Expliquer pourquoi on a: ${BD}↖{→}.{DC}↖{→}=0$ et ${DA}↖{→}.{DB}↖{→}=0$
2. A l'aide de la relation de Chasles, montrer que: ${BA}↖{→}.{BC}↖{→}=26$.
Méthode 2
1. Déterminer les distances BA et BC.
2. En n'utilisant que des distances, démontrer que: ${BA}↖{→}.{BC}↖{→}=26$.
Méthode 3
On se place dans un repère orthonormé $(D,{i}↖{→},{j}↖{→})$ tel que:
C a pour coordonnées (2,0), A a pour coordonnées (5,0), B a pour coordonnées (0,4).
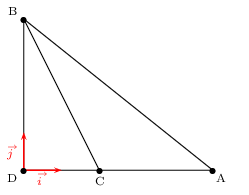
A l'aide de ces coordonnées, retrouver le fait que ${BA}↖{→}.{BC}↖{→}=26$.
Méthode 4
1.
Il est clair que les triangles ABD et CBD sont rectangles en D.
A l'aide de considérations trigonométriques, déterminer les angles géométriques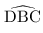 
et
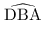arrondis au centième de degré près.
2.
On admet que: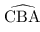 
= -
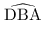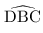
En déduire une valeur approchée de ${BA}↖{→}.{BC}↖{→}$.
Solution...
Corrigé
Méthode 1
1. Comme D est le projeté orthogonal de B sur (AC), les triangles ABD et CBD sont rectangles en D.
On a donc: ${BD}↖{→}.{DC}↖{→}=0$ et ${DA}↖{→}.{DB}↖{→}=0$
2. A l'aide de la relation de Chasles, on obtient:
${BA}↖{→}.{BC}↖{→}=({BD}↖{→}+{DA}↖{→}).({BD}↖{→}+{DC}↖{→})$
Soit: ${BA}↖{→}.{BC}↖{→}={BD}↖{→}.{BD}↖{→}+{BD}↖{→}.{DC}↖{→}+{DA}↖{→}.{BD}↖{→}+{DA}↖{→}.{DC}↖{→}$
Soit: ${BA}↖{→}.{BC}↖{→}={BD}↖{→}.{BD}↖{→}+0+0+{DA}↖{→}.{DC}↖{→}$ (d'après le 1.)
Or ${BD}↖{→}.{BD}↖{→}=BD^2$, et comme C appartient au segment [AD], on a: ${DA}↖{→}.{DC}↖{→}=DA ×DC$
Donc on obtient: ${BA}↖{→}.{BC}↖{→}=BD^2+DA ×DC$
Soit: ${BA}↖{→}.{BC}↖{→}=4^2+5 ×2$
Soit: ${BA}↖{→}.{BC}↖{→}=26$ c.q.f.d.
Méthode 2
1. Comme D est le projeté orthogonal de B sur (AC), les triangles ABD et CBD sont rectangles en D, et le théorème de Pythagore s'applique.
On obtient: $BA=√{BD^2+DA^2}=√{4^2+5^2}=√{41}$
Et de même: $BC=√{BD^2+DC^2}=√{4^2+25^2}=√{20}$
2.
On a: ${BA}↖{→}.{BC}↖{→}={1}/{2}(BA^2+BC^2-AC^2)$
Soit: ${BA}↖{→}.{BC}↖{→}={1}/{2}(41+20-3^2)$
Soit: ${BA}↖{→}.{BC}↖{→}=26$ c.q.f.d.
Méthode 3
On obtient facilement: ${BA}↖{→}(5;-4)$
et ${BC}↖{→}(2;-4)$
Le repère est orthonormé. Par conséquent, ${BA}↖{→}.{BC}↖{→}=5×2+(-4)×(-4)$
Soit: ${BA}↖{→}.{BC}↖{→}=26$ c.q.f.d.
Méthode 4
1.
Il est clair que les triangles ABD et CBD sont rectangles en D.
Par conséquent: $tan$ 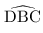$={DC}/{DB}$
Soit: $tan$ 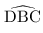$={2}/{4}=0,5$
Et par là (à la calculatrice): 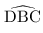$≈26,57°$
Et de même: $tan$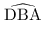$={DA}/{DB}={5}/{4}=1,25$
Et par là (à la calculatrice): 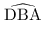$≈51,34°$
2.
On a: = -.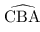
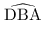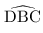Donc: 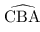$≈51,34°-26,57°≈24,77°$
Or ${BA}↖{→}.{BC}↖{→}=BA×BC×cos $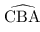
Donc: ${BA}↖{→}.{BC}↖{→}≈√{41}×√{20}×cos 24,77° $
Soit: ${BA}↖{→}.{BC}↖{→}≈26$
Cette dernière méthode ne donne qu'une valeur approchée du produit scalaire.