Produit scalaire dans le plan
Exercice 3
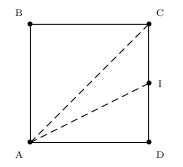
ABCD est un carré de côté 3. I est le milieu de $[CD]$.
Faire une figure.
Calculer les produits scalaires suivants:
${AB}↖{→}.{AD}↖{→}$
${AC}↖{→}.{AD}↖{→}$
${AC}↖{→}.{ID}↖{→}$
${AC}↖{→}.{AI}↖{→}$
Corrigé
ABCD est un carré, donc:
les vecteurs ${AB}↖{→}$ et ${AD}↖{→}$ sont orthogonaux (1)
${AD}↖{→}$ est le projeté orthogonal de ${AC}↖{→}$ sur ${AD}↖{→}$ (2)
Et comme I est le milieu de $[CD]$, on obtient:
${DC}↖{→}$ est le projeté orthogonal de ${AC}↖{→}$ sur ${ID}↖{→}$ (3)
et ${ID}↖{→}=-0,5{DC}↖{→}$ (4)
${AB}↖{→}.{AD}↖{→}=0$ (d'après (1))
${AC}↖{→}.{AD}↖{→}={AD}↖{→}.{AD}↖{→}$ (d'après (2))
Soit: ${AC}↖{→}.{AD}↖{→}=AD×AD=3×3=9$.
${AC}↖{→}.{ID}↖{→}={DC}↖{→}.{ID}↖{→}$ (d'après (3))
Donc: ${AC}↖{→}.{ID}↖{→}=-0,5{DC}↖{→}.{DC}↖{→}$ (d'après (4))
Soit: ${AC}↖{→}.{ID}↖{→}=-0,5×DC×DC=-0,5×3×3=-4,5$.
Il serait maladroit de projeter ${AC}↖{→}$ sur ${AI}↖{→}$ ou ${AI}↖{→}$ sur ${AC}↖{→}$ car ces projetés n'apparaissent pas naturellement sur le dessin.
On tente donc de faire apparaître des produits scalaires connus grace à la relation de Chasles
${AC}↖{→}.{AI}↖{→}={AC}↖{→}.({AD}↖{→}+{DI}↖{→})$ (d'après la relation de Chasles)
Donc: ${AC}↖{→}.{AI}↖{→}={AC}↖{→}.{AD}↖{→}+{AC}↖{→}.{DI}↖{→}$
Soit: ${AC}↖{→}.{AI}↖{→}=9-{AC}↖{→}.{ID}↖{→}$
Soit: ${AC}↖{→}.{AI}↖{→}=9-(-4,5)$
Soit: ${AC}↖{→}.{AI}↖{→}=13,5$