 Produit scalaire dans le plan
Produit scalaire dans le plan
Exercice 4
ABCD est un carré. F est sur le segment [BC]. B est sur le segment [AE]. Le triangle BEF est isocèle en B.
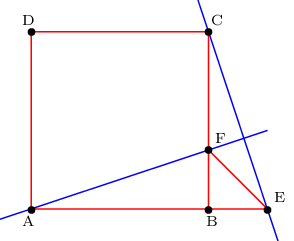
On notera que le triangle BEF est rectangle en B.
- Que peut-on conjecturer quant aux droites (AF) et (CE)?
- On rapporte le plan au repère orthonormé (A, B, D).
On pose $BE=x$.
Donner, sans justifier, les coordonnées des points A, B, C, D, E et F. - Montrer que le vecteur ${CE}↖{→}$ a pour coordonnées $(x;-1)$.
- Démontrer la conjecture du 1.
- Nous allons ici prouver la conjecture du 1. de façon plus élégante, sans utiliser de repère.
Il est clair que $AB=CB$ et $BF=BE$.
Expliquer pourquoi on a: ${AB}↖{→}.{CB}↖{→}=0$ et ${BF}↖{→}.{BE}↖{→}=0$.
Décomposer habilement les vecteurs ${AF}↖{→}$ et ${CE}↖{→}$ à l'aide de la relation de Chasles pour pouvoir calculer facilement le produit scalaire ${AF}↖{→}.{CE}↖{→}$.
Conclure.
Corrigé
- Conjecture: les droites (AF) et (CE) sont perpendiculaires.
- On rapporte le plan au repère orthonormé (A, B, D).
On pose $BE=x$.
On obtient: $A(0;0)$ $B(1;0)$ $C(1;1)$ $D(0;1)$ $E(1+x;0)$ $F(1;x)$.
- ${CE}↖{→}$ a pour coordonnées $(x_E-x_C;y_E-y_C)=(1+x-1;0-1)=(x;-1)$.
- ${AF}↖{→}$ a pour coordonnées $(1;x)$.
On calcule: ${AF}↖{→}.{CE}↖{→}=1×x+x×(-1)=x-x=0$
Donc les vecteurs ${AF}↖{→}$ et ${CE}↖{→}$ sont orthogonaux.
Donc les droites (AF) et (CE) sont perpendiculaires.
La conjecture du 1. est démontrée. -
ABCD est un carré, donc (AB) et (CB) sont perpendiculaires.
Donc les vecteurs ${AB}↖{→}$ et ${CB}↖{→}$ sont orthogonaux.
Donc: ${AB}↖{→}.{CB}↖{→}=0$.
De même, comme BEF est rectangle en B, on obtient: ${BF}↖{→}.{BE}↖{→}=0$.
On a: ${AF}↖{→}.{CE}↖{→}=({AB}↖{→}+{BF}↖{→}).({CB}↖{→}+{BE}↖{→})$ (d'après la relation de Chasles)
Soit: ${AF}↖{→}.{CE}↖{→}={AB}↖{→}.{CB}↖{→}+{AB}↖{→}.{BE}↖{→}+{BF}↖{→}.{CB}↖{→}+{BF}↖{→}.{BE}↖{→}$
Soit: ${AF}↖{→}.{CE}↖{→}=0+{AB}↖{→}.{BE}↖{→}+{BF}↖{→}.{CB}↖{→}+0$
Or, comme F est sur le segment [BC] et B est sur le segment [AE], on a:
${AB}↖{→}.{BE}↖{→}=AB×BE$ et ${BF}↖{→}.{CB}↖{→}=-BF×CB$
Donc on obtient: ${AF}↖{→}.{CE}↖{→}=AB×BE-BF×CB$
Or, comme ABCD est un carré, et que BEF est isocèle en B, on a: $AB=CB$ et $BE=BF$
Par conséquent: ${AF}↖{→}.{CE}↖{→}=AB×BE-BE×AB=0$
La conclusion est donc la même qu'à la question précédente.