 Produit scalaire dans le plan
Produit scalaire dans le plan
Exercice 5
EFG est un triangle tel que $EF=3$, $FG=8$ et $EG=9$.
1.a. Calculer le produit scalaire ${EF}↖{→}.{FG}↖{→}$.
1.b. En déduire la valeur de ${FE}↖{→}.{FG}↖{→}$.
1.c. En déduire une valeur arrondie au degré de l'angle géométrique ${F}↖{∧}$ du triangle EFG.
2.a. Soit I le milieu du segment $[EG]$.
Le théorème de la médiane permet d'obtenir facilement l'égalité: ${FE}↖{→}.{FG}↖{→}=FI^2-20,25$.
Expliquer comment.
Retrouver cette égalité sans utiliser ce théorème (conseil: exprimer le produit scalaire ${FE}↖{→}.{FG}↖{→}$ en fonction de la distance $FI$).
De façon analogue, prouver que: ${FE}↖{→}.{FG}↖{→}=2×FI^2-36,5$
2.b. En déduire la valeur de la distance $FI$.
3.a. Soit H le pied de la hauteur du triangle EFG issue de G.
Démontrer que ${FE}↖{→}$ et ${FH}↖{→}$ sont de sens opposés.
3.b. Calculer la distance $FH$.
Solution...Corrigé
Voici une figure convenable (mais non demandée)
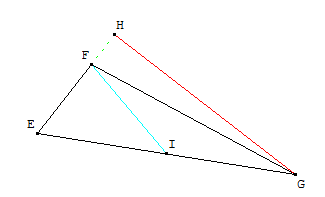
1.a. Les distances données dans l'énoncé insitent à utiliser une identité de polarisation.
(1) ${u}↖{→}.{v}↖{→}={1}/{2}\({∥{u}↖{→}+{v}↖{→}∥}^2-{∥{u}↖{→}∥}^2-{∥{v}↖{→}∥}^2\)\,\,\,\,\,\,\,\,$
ou (2) ${u}↖{→}.{v}↖{→}={1}/{2}\({∥{u}↖{→}∥}^2+{∥{v}↖{→}∥}^2-{∥{u}↖{→}-{v}↖{→}∥}^2\)\,\,\,\,\,\,\,\,$
Méthode 1: utilisons la première identité de polarisation.
${EF}↖{→}.{FG}↖{→}={1}/{2}({∥{EF}↖{→}+{FG}↖{→}∥^2}-{∥{EF}↖{→}∥^2}-{∥{FG}↖{→}∥^2})$
Soit: ${EF}↖{→}.{FG}↖{→}={1}/{2}({∥{EG}↖{→}∥^2}-EF^2-FG^2)$ (d'après la relation de Chasles)
Soit: ${EF}↖{→}.{FG}↖{→}={1}/{2}(EG^2-EF^2-FG^2)$
Soit: ${EF}↖{→}.{FG}↖{→}={1}/{2}(9^2-3^2-8^2)$
Soit: ${EF}↖{→}.{FG}↖{→}=4$
Méthode 2: utilisons la seconde identité de polarisation, mais avec ${GF}↖{→}$ à la place de ${FG}↖{→}$.
${EF}↖{→}.{GF}↖{→}={1}/{2}({∥{EF}↖{→}∥^2}+{∥{GF}↖{→}∥^2}- {∥{EF}↖{→}-{GF}↖{→}∥^2})$
${EF}↖{→}.{GF}↖{→}={1}/{2}({∥{EF}↖{→}∥^2}+{∥{GF}↖{→}∥^2}- {∥{EF}↖{→}+{FG}↖{→}∥^2})$
Soit: ${EF}↖{→}.{GF}↖{→}={1}/{2}(EF^2+GF^2-{∥{EG}↖{→}∥^2})$ (d'après la relation de Chasles)
Soit: ${EF}↖{→}.{GF}↖{→}={1}/{2}(EF^2+GF^2-EG^2)$
Soit: ${EF}↖{→}.{GF}↖{→}={1}/{2}(3^2+8^2-9^2)$
Soit: ${EF}↖{→}.{GF}↖{→}=-4$
Et donc: ${EF}↖{→}.{FG}↖{→}=4$
1.b. ${FE}↖{→}.{FG}↖{→}=-{EF}↖{→}.{FG}↖{→}=-4$.
Notons que le résultat étant négatif, l'angle ${F}↖{∧}$ (dans le triangle EFG) sera obtus.
1.c. On a: ${FE}↖{→}.{FG}↖{→}=FE×FG×\cos({F}↖{∧})$
Soit: $-4=3×8×\cos({F}↖{∧})$
Et donc: $-{4}/{24}=\cos({F}↖{∧})$
Soit: $\cos({F}↖{∧})=-{1}/{6}$

Nous cherchons un angle géométrique. A la calculatrice, nous obtenons ${F}↖{∧}≈100°$
2.a. Comme I est le milieu du segment $[EG]$, on obtient (d'après le théorème de la médiane):
${FE}↖{→}.{FG}↖{→}=FI^2-{1}/{4}EG^2$
Soit: ${FE}↖{→}.{FG}↖{→}=FI^2-{1}/{4}×9^2$
Soit: ${FE}↖{→}.{FG}↖{→}=FI^2-20,25$
Retrouvons cette égalité sans utiliser ce théorème de la médiane.
Comme I est le milieu de $[EG]$, on a:
${IG}↖{→}=-{IE}↖{→}=0,5{EG}↖{→}$ (1)
On calcule: ${FE}↖{→}.{FG}↖{→}=({FI}↖{→}+{IE}↖{→}).({FI}↖{→}+{IG}↖{→})$ (d'après la relation de Chasles)
Soit: ${FE}↖{→}.{FG}↖{→}={FI}↖{→}.{FI}↖{→}+{FI}↖{→}.{IG}↖{→}+{IE}↖{→}.{FI}↖{→}+{IE}↖{→}.{IG}↖{→}$
Soit: ${FE}↖{→}.{FG}↖{→}=FI^2+{FI}↖{→}.({IG}↖{→}+{IE}↖{→})-0,25×EG^2$ (d'après (1))
Soit: ${FE}↖{→}.{FG}↖{→}=FI^2+{FI}↖{→}.({0}↖{→})-0,25×EG^2$ (d'après (1))
Soit: ${FE}↖{→}.{FG}↖{→}=FI^2-0,25×81$
Soit: ${FE}↖{→}.{FG}↖{→}=FI^2-20,25$
Démontrons l'autre égalité proposée.
${FE}↖{→}.{FG}↖{→}={1}/{2}({∥{FE}↖{→}+{FG}↖{→}∥^2}-{∥{FE}↖{→}∥^2}-{∥{FG}↖{→}∥^2})$
Nous ne pouvons pas appliquer la relation de Chasles. Par contre, nous pouvons utiliser la règle du parallélogramme.
Nous obtenons alors: ${FE}↖{→}+{FG}↖{→}={FM}↖{→}$, où $M$ est un point tel que $FEMG$ soit un parallélogramme.
Mais comme I est le milieu de la diagonale $[EG]$, nous savons que ${FM}↖{→}=2.{FI}↖{→}$.
Par conséquent: ${FE}↖{→}+{FG}↖{→}=2.{FI}↖{→}$.
A retenir: si I est le milieu de $[EG]$, alors ${FE}↖{→}+{FG}↖{→}=2.{FI}↖{→}$.
Et par là: ${FE}↖{→}.{FG}↖{→}={1}/{2}({∥2.{FI}↖{→}∥^2}-{∥{FE}↖{→}∥^2}-{∥{FG}↖{→}∥^2})$
Soit: ${FE}↖{→}.{FG}↖{→}={1}/{2}(4×FI^2-FE^2-FG^2)$
Soit: ${FE}↖{→}.{FG}↖{→}={1}/{2}(4×FI^2-9-64)$
Soit: ${FE}↖{→}.{FG}↖{→}=2×FI^2-36,5$
L'égalité est différente de la première, mais elle donnera la même valeur de $FI$.
2.b. Utilisons la dernière égalité obtenue.
On a :${FE}↖{→}.{FG}↖{→}=2×FI^2-36,5$
Donc, d'après le 1.b. , $-4=2×FI^2-36,5$
Et par là: $16,25=FI^2$
Et comme une distance est positive: $FI=√16,25≈4,03$.
La première égalité obtenue donne le même résultat; vous pouvez vérifiez!

3.a. Soit H le pied de la hauteur du triangle EFG issue de G.
Donc H est le projeté orthogonal de G sur $(EF)$.
Donc: ${FE}↖{→}.{FG}↖{→}={FE}↖{→}.{FH}↖{→}$
Soit: $-4={FE}↖{→}.{FH}↖{→}$
Comme ce produit est négatif, les vecteurs colinéaires ${FE}↖{→}$ et ${FH}↖{→}$ sont de sens opposés.
3.b. On obtient donc: $-4=-FE×FH$
Soit: $-4=-3×FH$
Et par là: $FH={4}/{3}≈1,33$