 Produit scalaire dans le plan
Produit scalaire dans le plan
Exercice 6
Soient A et B deux points et I le milieu de [AB].
1.a. Soit M un point quelconque. Rappeler le théorème de la médiane.
1.b. Soit M un point quelconque. A l'aide de la relation de Chasles, montrer que: $MA^2+MB^2=2MI^2+{AB^2}/{2}$.
On suppose par la suite que $AB=4$.
2.a. Déterminer l'ensemble $E_1$ des points M du plan tels que ${MA}↖{→}.{MB}↖{→}=3$
2.b. Déterminer l'ensemble $E_2$ des points M du plan tels que $MA^2+MB^2=7$
3. Déterminer l'ensemble $E_3$ des points M du plan tels que ${AM}↖{→}.{AB}↖{→}=3$.
Le point H, pied de la hauteur du triangle ABM issue de M, peut servir...
Solution...
Corrigé
Soient A et B deux points et I le milieu de [AB].
1.a. Soit M un point quelconque. Comme I est le milieu de [AB], on obtient (d'après le théorème de la médiane):
${MA}↖{→}.{MB}↖{→}=MI^2-{1}/{4}AB^2$
1.b. Soit M un point quelconque. A l'aide de la relation de Chasles, on obtient:
$MA^2+MB^2={MA}↖{→}^2+{MB}↖{→}^2=({MI}↖{→}+{IA}↖{→})^2+({MI}↖{→}+{IB}↖{→})^2$
Soit: $MA^2+MB^2={MI}↖{→}^2+2{MI}↖{→}.{IA}↖{→}+{IA}↖{→}^2+{MI}↖{→}^2+2{MI}↖{→}.{IB}↖{→}+{IB}↖{→}^2$
Soit: $MA^2+MB^2=2MI^2+2{MI}↖{→}.({IA}↖{→}+{IB}↖{→})+IA^2+IB^2$
Or, comme I est le milieu de [AB], on a: ${IA}↖{→}+{IB}↖{→}={0}↖{→}$ et $IA=IB={AB}/{2}$
Donc on obtient: $MA^2+MB^2=2MI^2+2{MI}↖{→}.{0}↖{→}+2({AB}/{2})^2$
Et par là: $MA^2+MB^2=2MI^2+0+2({AB}^2/{4})$
Soit: $MA^2+MB^2=2MI^2+{AB^2}/{2}$.
On suppose désormais que $AB=4$.
2.a. On a: ${MA}↖{→}.{MB}↖{→}=3$ $⇔$ $MI^2-{1}/{4}AB^2=3$
Soit: ${MA}↖{→}.{MB}↖{→}=3$ $⇔$ $MI^2-{16}/{4}=3$
Soit: ${MA}↖{→}.{MB}↖{→}=3$ $⇔$ $MI^2=7$
Donc $E_1$ est le cercle de centre I de rayon $√{7}$
2.b. On a: $MA^2+MB^2=7$ $⇔$ $2MI^2+{AB^2}/{2}=7$
Soit: $MA^2+MB^2=7$ $⇔$ $2MI^2+{16}/{2}=7$
Soit: $MA^2+MB^2=7$ $⇔$ $MI^2=-0,5$
Comme un carré ne peut être strictement négatif, l'égalité est impossible.
Donc $E_2$ est l'ensemble vide.
3.
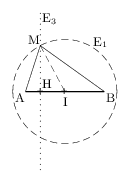
Soit H le projeté orthogonal de M sur la droite (AB).
On note que les vecteurs ${AH}↖{→}$ et ${AB}↖{→}$ sont donc colinéaires.
On a: ${AM}↖{→}.{AB}↖{→}=3$ $⇔$ ${AH}↖{→}.{AB}↖{→}=3$
Comme ce dernier produit scalaire est positif, les vecteurs colinéaires ${AH}↖{→}$ et ${AB}↖{→}$ sont de même sens.
On obtient alors: $AH×AB=3$.
Soit $AH×4=3$, et donc: $AH=0,75$.
Il est donc clair que, pour tout point M, le point H se situe sur le segment [AB], à une distance égale à 0,75 de A.
L'ensemble $E_3$ est alors la droite passant par H et perpendiculaire à la droite (AB).