Suites
Exercice 1
- Pour tout naturel $n$, $u_{n}$ est le nombre de billes rouges de la figure de rang $n$ obtenue comme ci-dessous.
Ainsi, $u_1=2$ et $u_2=6$.
Que valent $u_3$, $u_4$ et $u_5$?
Que vaudrait $u_6$?
Définir (sans justifier) la suite $(u_n)$ de façon explicite. -
On peut observer que les billes de chaque motif forment un rectangle, lui même composé de 2 triangles.
Par exemple, pour $u_5$, cela donne:
En déduire alors l'expression de $1+2+3+4+5$ en fonction de $u_5$.
Puis donner (sans justifier) la formule générale donnant $1+2+3+...+n$ en fonction du naturel $n$. 
On considère le programme en Python ci-dessous.
Faire fonctionner ce programme "à la main" pour $n=2$ (en précisant les valeurs successives prises par les variables).
Donner les valeurs de $u_1$, $u_2$, $u_3$, $u_4$ et $u_5$. Que constate-t-on?-
Le dessin de la première question est produit par le programme en Python ci-dessous.
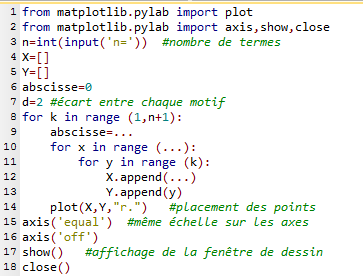
Compléter les lignes 9, 10 et 12 de ce programme pour qu'il fonctionne correctement.
Corrigé
- On constate que: $u_3=12$, $u_4=20$ et $u_5=30$
A priori: $u_6=6×7=42$
On conjecture que $u_n=n×(n+1)$ pour tout naturel non nul $n$.
Cette suite s'appelle la suite des nombres oblongs. -
$u_5$ est représenté ci-dessous.
Chacun des 2 triangles possède $1+2+3+4+5$ billes. Donc: $1+2+3+4+5={u_5}/{2}$
Généralisons cela pour tout naturel $n$ non nul.
On a: $u_n=n×(n+1)$.
On conjecture donc que $1+2+3+...+n={n×(n+1)}/{2}$ pour tout naturel non nul $n$.
On verra que ce résultat fera partie du cours sur les suites arithmétiques. - Fonctionnement du programme "à la main" pour $n=2$.
n=5
k=1 (première boucle)
u=0
x=0 y=0 u=0+1=1
x=1 y=0 u=1+1=2
il s'affiche u_1=2
k=1 (seconde et dernière boucle)
u=0
x=0 y=0 u=0+1=1 y=1 u=1+1=2
x=1 y=0 u=2+1=3 y=1 u=3+1=4
x=2 y=0 u=4+1=5 y=1 u=5+1=6
il s'affiche u_2=6
On obtient: $u_1=2$, $u_2=6$, $u_3=12$, $u_4=20$ et $u_5=30$
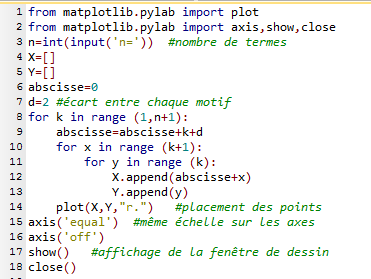
On conjecture que la suite ($u_n)$ est la même que celle de la question 1. - Voici le programme en Python complété correctement.
