 Suites
Suites
Exercice 11
La suite $(u_n)$ est définie par $u_n=(-28)×0,6^n+35$ pour tout entier naturel $n$.
1. On considère l'algorithme suivant:
Lire $N$
$S$ $←$ 0
Pour $I$ allant de 0 à$ N$
$S$ $←$ $-28×0,6^N+35$
Fin du Pour
Afficher $N$
Corriger l'algorithme proposé pour qu'il permette de déterminer la valeur de la somme $u_0+u_1+...+u_n$ pour tout entier naturel $n$. Proposer un programme convenable en PYTHON.
2.a. On considère l'algorithme suivant:
$U$ $←$ 7
$N$ $←$ 0
Tant que $U>30$
$N$ $←$ $N+$1
$U$ $←$ $-28×0,6^N+35$
Fin du Tant que
Afficher $U$
Corriger l'algorithme proposé pour qu'il permette de déterminer la plus petite valeur de $n$ à partir de laquelle les termes de la suite $(u_n)$ sont strictement supérieurs à 30. Proposer un programme convenable en PYTHON.
2.b. Que suffirait-il de démontrer pour être certain que la valeur de $n$ fournie par cet algorithme est bien la valeur cherchée?
2.c. Démontrer votre proposition.
Corrigé
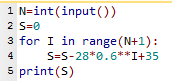
1. Voici un l'algorithme correct:
Lire $N$
$S$ $←$ 0
Pour $I$ allant de 0 à $ N$
$S$ $←$ $S-28×0,6^I+35$
Fin du Pour
Afficher $S$
Voici un programme convenable.
2.a. Voici un l'algorithme correct:
$U$ $←$ 7
$N$ $←$ 0
Tant que $U≤30$
$N$ $←$ $N+$1
$U$ $←$ $-28×0,6^N+35$
Fin du Tant que
Afficher $N$
Voici un programme convenable.

2.b. Il suffirait de démontrer que la suite $(u_n)$ est strictement croissante.
2.c. Comme $0$<$0,6$<$1$, la suite géométrique $(0,6^n)$ est strictement décroissante.
Or $-28$<$0$, et par là, la suite géométrique $(-28×0,6^n)$ est strictement croissante.
Et finalement, la suite $(u_n)$ est également strictement croissante.