 Suites
Suites
Exercice 12
Au mois de janvier 2000, le loyer payé par Isidore s'élève à $300$ euros. Ce loyer augmente chaque mois de 0,2%.
Soit $u_n$ le loyer payé (en euros) au bout de $n$ mois. Ainsi, $u_0=300$.
On admet que $\lim↙{n→+∞}u_n=+∞$
1.a. Exprimer $u_{n+1}$ en fonction de $u_n$ pour tout naturel $n$.
1.b. Qu'en déduire concernant la suite $(u_n)$?
1.c. Exprimer $u_{n}$ en fonction de $n$ .
1.d. Donner le sens de variation de $(u_n)$.
2.a. Pourquoi existe-t-il une valeur de $n$ à partir de laquelle tous les $u_n$ sont strictement supérieurs à 400?
2.b. Ecrire l'algorithme d'un programme permettant de déterminer la plus petite valeur $n_0$ telle que $u_{n_0}>400$.
2.c. Programmer un tel programme en PYTHON sur votre calculatrice ou votre ordinateur. Donner la valeur de $n_0$ affichée par le programme après exécution.
2.d. Si $n>n_0$, alors $u_n>400$. Pourquoi?
3. Combien Isidore a-t-il dépensé en loyers du premier janvier 2000 au 31 décembre 2013?
Corrigé
1.a. Pour tout naturel $n$: $u_{n+1}=u_n+{0,2}/{100}×u_n=(1+{0,2}/{100})×u_n=1,002×u_n$.
1.b. Par conséquent, la suite $(u_n)$ est géométrique de raison 1,002 de premier terme $u_0=300$.
1.c. Et par là, pour tout naturel $n$: $u_n=300× 1,002^n$.
1.d. Comme $1$<$1,002$, alors $(1,002^n)$ est strictement croissante.
Et comme $300$>$0$, $(u_n)$ est également strictement croissante.
2.a. Il existe une valeur de $n$ à partir de laquelle tous les $u_n$ sont strictement supérieurs à 400 car $\lim↙{n→+∞}u_n=+∞$
Attention! Ne pas justifier en utilisant la stricte croissance de la suite!
2.b. Nous proposons deux algorithmes possibles.
Le premier utilise
la formule de récurrence.
N $←$ 0
U $←$ $300$
Tant que U$≤400$
U $←$ U$× 1,002$
N $←$ N+1
Fin du Tant que
Afficher N
Le second utilise
la formule explicite.
N $←$ 0
Tant que $300× 1,002^N≤400$
N $←$ N+1
Fin du Tant que
Afficher N
2.c.
Exemple de programme utilisant la formule de récurrence:
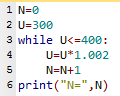
Le programme donnent une valeur de N égale à 144.
2.d. Si $n>n_0$, alors $u_n>u_{n_0}$ car la suite $(u_n)$ est strictement croissante.
Et comme $u_{n_0}>400$, on obtient: $u_n>400$.
Attention! Ne pas justifier en utilisant la limite de la suite!
3.
Le mois de janvier 2000 correspond à $n=0$.
Le mois de décembre 2000 correspond à $n=11$.
Le mois de décembre 2001 correspond à $n=11+1×12=23$.
Le mois de décembre 2013 correspond à $n=11+13×12=167$.
On cherche donc la somme $S=u_0+u_1+u_2+...+u_167$.
Et comme $(u_n)$ est géométrique de raison 1,002 de premier terme $u_0=300$, on a:
$S=u_0× {1-1,002^{167+1}}/{1-1,002}=300× {1-1,002^{168}}/{-0,002}≈59\,830,43$.
Pendant les 14 ans considérés, Isidore a dépensé $59\,830,43$ euros en loyers.