 Suites
Suites
Exercice 13
La suite de Syracuse $(u_n)$ d'un nombre entier $N$ > $0$ est définie par récurrence, de la manière suivante :
$u_0=N$
pour tout entier naturel $n$:
si $u_n$ est pair, alors $u_{n+1}={u_n}/{2}$ .
si $u_n$ est impair, alors $u_{n+1}=3u_n+1$,
La conjecture de Syracuse affirme que, pour tout entier naturel $N$, il existe un entier naturel $n$ tel que $u_{n}=1$.
1. Posons $N=1$
Déterminer $u_n$ pour $n$ allant de 1 à 6
On admettra par la suite que, pour toute suite de Syracuse, après que le nombre 1 a été atteint, la suite des valeurs (1,4,2,1,4,2…) se répète indéfiniment en un cycle de longueur 3.
2. Posons $N=3$
Déterminer $u_n$ pour $n$ allant de 1 à 11
3. A chaque suite de Syracuse, on associe 3 nombres particuliers:
- le temps de vol : c'est le plus petit indice $n$ tel que $u_n = 1$. Quelle est sa valeur pour la suite de Syracuse de 3?
- le temps de vol en altitude : c'est le plus petit indice $n$ tel que $u_{n+1}$<$ u_0$. Quelle est sa valeur pour la suite de Syracuse de 3?
- l'altitude maximale : c'est la valeur maximale de la suite. Quelle est sa valeur pour la suite de Syracuse de 3?
4. Le programme suivant, écrit dans le langage Python, permet de déterminer le temps de vol d'une suite de Syracuse de nombre $N$.
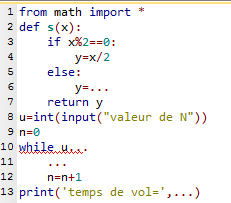
Compléter les parties manquantes, puis faites fonctionner ce programme sur votre ordinateur pour $N=127$. Qu'affiche-t-il alors?
Corrigé
1.
$u_0=1$
1 est impair; donc: $u_1=3×1+1=4$
4 est pair; donc: $u_2={4}/{2}=2$
2 est pair; donc: $u_3={2}/{2}=1$
1 est impair; donc: $u_4=3×1+1=4$
4 est pair; donc: $u_5={4}/{2}=2$
2 est pair; donc: $u_6={2}/{2}=1$
2.
$u_0=3$
3 est impair; donc: $u_1=3×3+1=10$
10 est pair; donc: $u_2={10}/{2}=5$
5 est impair; donc: $u_3=3×5+1=16$
16 est pair; donc: $u_4={16}/{2}=8$
8 est pair; donc: $u_5={8}/{2}=4$
4 est pair; donc: $u_6={4}/{2}=2$
2 est pair; donc: $u_7={2}/{2}=1$
1 est impair; donc: $u_8=3×1+1=4$
4 est pair; donc: $u_9={4}/{2}=2$
2 est pair; donc: $u_{10}={2}/{2}=1$
1 est impair; donc: $u_{11}=3×1+1=4$
3. D'après les résultats du 2.:
- le temps de vol de la suite de Syracuse de 3 vaut 7.
- le temps de vol en altitude de la suite de Syracuse de 3 vaut 5 (car, pour $n≤5$, on a: $u_n≥u_0$, et $u_{5+1}$<$u_0$)
- l'altitude maximale de la suite de Syracuse de 3 vaut 16.
4. Voici le programme correct.
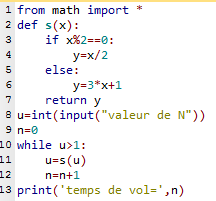
Pour $N=127$, il affiche 46.
Le temps de vol de la suite de Syracuse de 3 vaut 46.