 Suites
Suites
Exercice 8
L'entreprise InfoPub a consommé 100 000 KWh d'électricité l'année 2000. Puis elle a décidé de diminuer de $1,5%$ par an sa consommation d'électricité annuelle à partir de l'année 2001,
et elle y a réussi parfaitement jusqu'à l'année 2020 comprise.
Soit $u_n$ la consommation d'électricité annuelle de l'entreprise InfoPub pour l'année $2000+n$ (en KWh).
Ainsi, on a: $u_0=100\,000$.
- Montrer que $u_2=97\,022,5$.
- Déterminer la nature de la suite $(u_n)$.
- Pour tout entier naturel $n$, exprimer $u_n$ en fonction de $n$.
- Quelle est la consommation d'électricité annuelle de l'entreprise InfoPub pour l'année $2020$ (arrondie à 0,01KWh)?
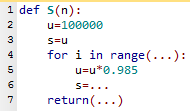
- Compléter le programme ci-dessous (en PYTHON) pour que la fonction renvoie la consommation totale de l'entreprise InfoPub pour les années 2000 à 2020 (incluses) si l'on entre l'instruction $S(20)$.
Remplacer les ... des lignes 4, 6 et 7 par ce qu'il faut pour que la fonction soit convenable.
- On désire retrouver le résultat précédent sans utiliser de programme.
Calculer directement la somme $S(20)=u_0+u_1+u_2+...+u_{20}$ (arrondie à 0,01)
Corrigé
- Le coefficient multiplicateur correspondant à une baisse de $1,5%$ vaut $98,5%$.
On a alors: $u_1=u_0×0,985=100\,000×0,985=98\,500$.
Et: $u_2=u_1×0,985=98\,500×0,985=$$97\,022,5$. - Pour tout entier naturel $n$, on a: $u_{n+1}=0,985×u_n$.
Donc $(u_n)$ est géométrique de raison 0,985.
-
Par conséquent, pour tout entier naturel $n$, on a: $u_n=u_0×0,985^n$
Soit: $u_n= 100\,000×0,985^n$. - On calcule: $u_{20}= 100\,000×0,985^{20}≈73\,913,64$ Donc la consommation d'électricité annuelle de l'entreprise InfoPub pour l'année $2020$ est d'environ $73\,913,64$ KWh.
- Voici le programme complété correctement.
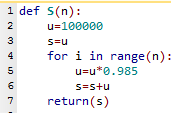
ligne 4: si n vaut 20, i va varier de 0 à 19 . La boucle for sera alors parcourue 20 fois.
ligne 6: la valeur de s est augmentée de la valeur courante de u
ligne 7: la valeur renvoyée par la fonction est la dernière valeur de s après la boucle.
Pour faire apparaître la valeur de S(20), soit vous écrivez S(20) directement dans la console (après avoir exécuté le programme), soit vous ajoutez print(S(20)) après la définition de S(n) et vous exécutez le programme. - On a: $S(20)=u_0+u_1+u_2+...+u_{20}=u_0+u_0×0,985+u_0×0,985^2+...+u_0×0,985^{20}$
Soit: $S(20)=u_0(1+0,985+0,985^2+...+0,985^{20})$
Soit: $S(20)=100\,000{1-0,985^{21}}/{1-0,985}$
Soit: $S(20)≈1\,813\,004,09$