Fonctions trigonométriques
Exercice 1
Le plan est rapporté au repère orthonormé direct (O,I,J).
Par enroulement de la droite des réels sur le cercle trigonométrique, on peut associer à tout réel $x$ un unique point M sur le cercle trigonométrique.
A ce point M correspond un angle géométrique 
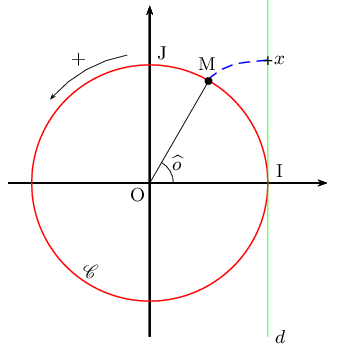
Les mesures qui suivent concernent l'angle géométrique
Partie 1.
Les affirmations suivantes sont-elles vraies?
- Une mesure égale à $60°$ correspond à une mesure égale à ${π}/{6}$ (en radians).
- Une mesure égale à $45°$ correspond à une mesure égale à ${π}/{4}$ (en radians).
- Une mesure égale à $30°$ correspond à une mesure égale à ${2π}/{3}$ (en radians).
- Les réels ${π}/{6}$ et ${13π}/{6}$ sont associés au même point sur le cercle trigonométrique.
Partie 2.
Les affirmations suivantes sont-elles vraies?
- Si le point M du cercle trigonométrique est associé au réel ${5π}/{6}$, alors une mesure de l'angle géométrique
est 135°.
- Les réels ${5π}/{6}$ et $-{5π}/{6}$ correspondent au même angle géométrique.
- Une mesure égale à $135°$ correspond à une mesure égale à ${3π}/{4}$ (en radians).
Corrigé
Partie 1.
- C'est FAUX.
Une mesure égale à $60°$ correspond à une mesure égale à ${π}/{3}$ (en radians). - C'est VRAI.
Une mesure égale à $45°$ correspond effectivement à une mesure égale à ${π}/{4}$ (en radians). - C'est FAUX.
Une mesure égale à $30°$ correspond à une mesure égale à ${π}/{6}$ (en radians). - C'est VRAI.
En effet: ${13π}/{6}-{π}/{6}=2π$; on a bien obtenu un multiple de $2π$ (lui-même).
Partie 2.
- C'est FAUX.
Si le point M du cercle trigonométrique est associé au réel ${5π}/{6}$, alors, comme ${5π}/{6}=π-{π}/{6}$, une mesure de l'angle géométrique est 180°-30°=150°. - C'est VRAI.
Les réels ${5π}/{6}$ et $-{5π}/{6}$ sont dans $[-π;π]$ et ils ont la même valeur absolue. Ils correspondent au même angle géométrique de mesure ${5π}/{6}$, soit 150°.
On notera qu'ils correspondent à deux points M du cercle trigonométrique symétriques par rapport à l'axe des abscisses.
. - C'est VRAI.
Comme $135°=90°+45°$, une mesure égale à $135°$ correspond à une mesure égale à ${π}/{2}+{π}/{4}={3π}/{4}$ (en radians).