Fonctions trigonométriques
Exercice 2
Dans cet exercice, toutes les mesures sont exprimées en radians.
Soit $x$ un réel associé à un point M du cercle trigonométrique par enroulement de la droite des réels.
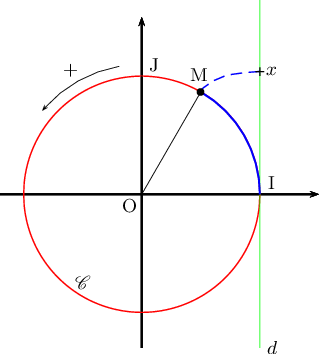
Tous les réels du type $x+k×2π$, où $k$ est en entier relatif, correspondent au même point M que le réel $x$.
On appellera mesure principale de $x$ le seul nombre de type $x+k×2π$, où $k$ est en entier relatif, situé dans
l'intervalle $]-π;π]$.
Par exemple, comme ${π}/{3}={19π}/{3}-3×2π$, et comme ${π}/{3}$ est dans $]-π;π]$, la mesure principale de ${19π}/{3}$ est ${π}/{3}$.
On notera que tout $x$ de $]-π;π]$ est la mesure principale de $x+k×2π$ pour n'importe quel entier relatif $k$.
Une mesure principale est en fait la longueur de l'arc de cercle le plus petit allant de I vers M, cette longueur étant comptée négativement si M est en dessous de l'axe des
abscisses.
Deux réels ont même mesure principale si et seulement si ils sont associés au même point M du cercle trigonométrique par enroulement de la droite des réels.
Remarque: le terme "mesure principale" est en fait associé à un "angle orienté" ( mais cette notion est hors programme ). Nous confondons ici les angles orientés et leurs mesures.
.
- On suppose que $a=2π$. Déterminer la mesure principale de $a$.
- On suppose que $a=-π$. Déterminer la mesure principale de $a$.
- On suppose que $a={27π}/{6}$. Déterminer la mesure principale de $a$.
-
On suppose que $a={10π}/{3}$. Déterminer la mesure principale de $a$. - On suppose que $a={121π}/{4}$ et que $b=-{15π}/{4}$. Les réels $a$ et $b$ ont-ils la même mesure principale?
Corrigé
On rappelle que $2π$ correspond à un "tour" complet du cercle trigonométrique (dans le sens positif).
- On a: $2π=0+2π$. Et comme la valeur $0$ est située dans l'intervalle $]-π;π]$, c'est la mesure principale de $a$.
- On a: $-π=π-2π$. Et comme la valeur $π$ est située dans l'intervalle $]-π;π]$, c'est la mesure principale de $a$.
- On a: $2π={12π}/{6}$.
On écrit alors: ${27π}/{6}=2×{12π}/{6}+{3π}/{6}=2×2π+{π}/{2}$.
Et comme la valeur ${π}/{2}$ est située dans l'intervalle $]-π;π]$, c'est la mesure principale de $a$.
A retenir: pour repérer le nombre de "tours" pour atteindre la mesure principale, il suffit d'écrire $2π$ sous la forme d'une fraction convenable.
- On a: $2π={6π}/{3}$.
On écrit alors: ${10π}/{3}={6π}/{3}+{4π}/{3}=2π+{4π}/{3}$.
Mais , comme ${4π}/{3}>π$, la mesure ${4π}/{3}$ n'est pas une mesure principale.
On doit faire un tour de plus!
On écrit alors: ${10π}/{3}=2×{6π}/{3}-{2π}/{3}$.
Cette fois, on a bien: $-π$<$-{2π}/{3}≤π$.
La valeur $-{2π}/{3}$ est située dans l'intervalle $]-π;π]$; c'est la mesure principale de $a$. - Si la différence des réels proposés correspond à un nombre entier de "tours" du cercle trigonométrique,
alors les deux réels sont associées à un même point M du cercle trigonométrique,
et par là, ils auront la même mesure principale.
On calcule: ${121π}/{4}-(-{15π}/{4})={121π}/{4}+{15π}/{4}={136π}/{4}=34π=17×2π$.
La différence est bien un multiple de $2π$.
Donc $a$ et $b$ ont effectivement la même mesure principale.
Pour les curieux, j'ai calculé la mesure pricipale:
${121π}/{4}=15×{8π}/{4}+{π}/{4}=15×2π+{π}/{4}$.
Et comme la valeur ${π}/{4}$ est située dans l'intervalle $]-π;π]$, c'est la mesure principale de $a$ (et de $b$).