La Spécialité Maths en Première

Corrigé

Chacun doit connaître parfaitement le schéma ci-desous.

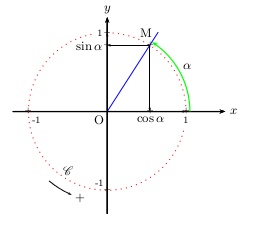
A savoir également:
Pour tout réel $x$, pour tout entier relatif $k$, on a:
$\cos (x+k×2π)=\cos (x)$
$\sin (x+k×2π)=\sin (x)$

  $\cos 0=1$    $\cos{π}/{6}={√3}/{2}$    $ \cos{π}/{4}={√2}/{2}$    $\cos{π}/{3}={1}/{2}$    $\cos{π}/{2}=0$
  $\sin 0=0$    $\sin{π}/{6}={1}/{2}$    $ \sin{π}/{4}={√2}/{2}$    $\sin{π}/{3}={√3}/{2}$    $\sin{π}/{2}=1$

1. $a=\cos(2π)+\sin(2π)=\cos (0+2π)+\sin (0+2π)=\cos 0+\sin 0=1+0=1$.


2. $b=\cos({π}/{3})+\sin({π}/{6})={1}/{2}+{1}/{2}=1$.


3. $c=\cos({π}/{4})+\sin(π)={√2}/{2}+0={√2}/{2}$.


4. $d=\cos({7π}/{3})+\sin(3π)=\cos({7π}/{3}-2π)+\sin(3π-2π)=\cos({π}/{3})+\sin(π)={1}/{2}+0={1}/{2}$.


5. $e=\cos^2({π}/{7})+\sin^2({π}/{7})=1$.
   A retenir: pour tout réel $x$, on a: $\cos^2(x)+\sin^2(x)=1$