Fonctions trigonométriques
Exercice 4
On considère la fonction $f$ définie sur $ℝ$ et représentée graphiquement ci-dessous dans un repère orthonormé.
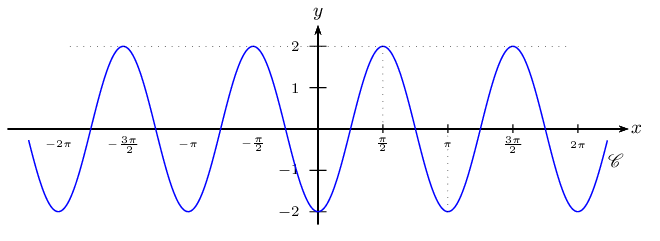
1.a. Graphiquement, déterminer la parité de $f$.
1.b. Graphiquement, déterminer si $f$ est périodique.
1.c. Graphiquement, déterminer $f(0)$ et $f({π}/{4})$.
2.
On admet désormais que $f(x)=2\cos(2x+π)$.
Retrouver algébriquement les résultats trouvés aux questions précédentes.
Solution...
Corrigé
1.a. On conjecture graphiquement que la fonction $f$ est paire, car il semble que $\C$ soit symétrique par rapport à l'axe des ordonnées.
1.b. On conjecture graphiquement que la fonction $f$ est périodique, car le même "motif" semble se répèter indéfiniment. Sa période serait $π$ car le plus petit motif répété a pour largeur $π$.
1.c. Graphiquement, on obtient: $f(0)=-2$ et $f({π}/{2})=0$.
2.
On admet désormais que $f(x)=2\cos(2x+π)$.
Avant tout, on remarque que: $f(x)=-2\cos(2x)$
A retenir: pour tout $a$, $\cos(a+π)=-\cos(a)$
2.a. Le domaine de définition de $f$ est $ℝ$; il est bien symétrique par rapport à $0$.
Par ailleurs, pour tout $x$ de $ℝ$, on a:
$f(-x)=-2\cos(2×(-x))=-2\cos(-2x)=-2\cos(2x)$
Soit: $f(-x)=f(x)$.
Par conséquent, la fonction $f$ est paire.
A retenir: pour tout $a$, $\cos(-a)=\cos(a)$
2.b. Montrons que la fonction $f$ est périodique de période $π$.
pour tout $x$ de $ℝ$, on a:
$f(x+π)=-2\cos(2×(x+π))=-2\cos(2x+2π)=-2\cos(2x)$
Soit: $f(x+π)=f(x)$.
Par conséquent, la fonction $f$ est bien périodique de période $π$.
A retenir: pour tout $a$, pour tout relatif $k$, $\cos(a+2kπ)=\cos(a)$
2.c. On calcule:
$f(0)=-2\cos(2×0)=-2\cos (0)=-2×1=-2$
$f({π}/{4})=-2\cos(2×{π}/{4})=-2\cos({π}/{2})=-2×0=0$.