Fonctions trigonométriques
Exercice 5
1.a. Déterminer $\sin{5π}/{6}$, $\cos{3π}/{4}$, $\sin{2π}/{3}$.
2. Déterminer $\cos{-5π}/{6}$, $\sin{-3π}/{4}$, $\sin{-2π}/{3}$.
3. Déterminer $\cos{7π}/{6}$ et $\sin{7π}/{6}$.
4. Déterminer $\cos{13π}/{6}$ et $\sin{37π}/{3}$.
Solution...Corrigé
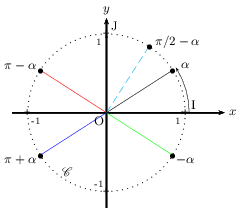
1.a. $\sin{5π}/{6}=\sin (π-{π}/{6})=\sin{π}/{6}={1}/{2}$
$\cos{3π}/{4}=\cos(π-{π}/{4})=-\cos{π}/{4}=-{√2}/{2}$
$\sin{2π}/{3}=\sin(π-{π}/{3})=\sin{π}/{3}={√3}/{2}$
2. $\cos{-5π}/{6}=\cos{5π}/{6}=\cos (π-{π}/{6})=-\cos{π}/{6}=-{√3}/{2}$
$\sin{-3π}/{4}=-\sin{3π}/{4}=-(\sin(π-{π}/{4}))=-\sin{π}/{4}=-{√2}/{2}$
$\sin{-2π}/{3}=-\sin{2π}/{3}=-(\sin(π-{π}/{3}))=-\sin{π}/{3}=-{√3}/{2}$
3. $\cos{ 7π}/{6}=\cos(π+{ π}/{6})=-\cos{ π}/{6}=-{√3}/{2}$
$\sin{ 7π}/{6}=\sin(π+{ π}/{6})=-\sin{ π}/{6}=-0,5$
4. $\cos{ 13π}/{6}=\cos({ 12π}/{6}+{π}/{6})=\cos(2π+{π}/{6})=\cos{π}/{6}={√3}/{2}$
$\sin{37π}/{3}=\sin({36π}/{3}+{π}/{3})=\sin(6×2π+{π}/{3})=\sin{π}/{3}={√3}/{2}$.