Fonctions trigonométriques
Exercice 7
Soit $x$ un réel de l'intervalle $[-π;-{π}/{2}]$. Et soit M le point du cercle trigonométrique associé à $x$.
1. Placer le point M tel que $\sin x=-{5}/{9}$
2. Placer les points du cercle trigonométrique associés aux réels:
${π}/{2}+x$ ${π}/{2}-x$ $π+x$ $π-x$
3. Déterminer la valeur de $\cos x$.
4. Déterminer les valeurs exactes de:
$\sin ({π}/{2}-x)$ $\cos ({π}/{2}-x)$
$\sin (π+x)$ $\cos (π-x)$
Corrigé
1. $x$ est dans $[-π;-{π}/{2}]$. Donc le point M associé à $x$ est dans le troisième quadrant.
Et comme $\sin x=-{5}/{9}≈-0,56$, on a ainsi l'ordonnée de ce point M.
D'où le dessin ci-dessous.
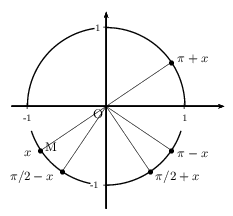
2. Les points du cercle trigonométrique associés aux réels:
${π}/{2}+x$ ${π}/{2}-x$ $π+x$ $π-x$
sont placés sur la figure précédente.
3. On a: $\cos^2 x+\sin^2 x=1$.
Donc: $\cos^2 x=1-\sin^2 x$
Soit: $\cos^2 x=1-(-{5}/{9})^2=1-{25}/{81}={56}/{81}$
Or, comme $x$ est dans $[-π;-{π}/{2}]$, on a: $\cos x$<$0$.
Donc: $\cos x=-√{{56}/{81}}=-{2√{14}}/{9}≈-0,83$
4. On utilise le propriétés des angles associés.
$\sin ({π}/{2}-x)=\cos x=-{2√{14}}/{9}$ $\cos ({π}/{2}-x)=\sin x=-{5}/{9}$
$\sin (π+x)=-\sin x={5}/{9}$ $\cos (π-x)=-\cos x={2√{14}}/{9}$